题目内容
在平面直角坐标系xOy中,已知抛物线y=ax2+bx-2经过(2,1)和(6,-5)两点.
(1)求抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,点P是在直线x=4右侧的此抛物线上一点,过点P作PM⊥x轴,垂足为M.若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
(3)点E是直线BC上的一点,点F是平面内的一点,若要使以点O、B、E、F为顶点的四边形是菱形,请直接写出点F的坐标.

(1)求抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,点P是在直线x=4右侧的此抛物线上一点,过点P作PM⊥x轴,垂足为M.若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
(3)点E是直线BC上的一点,点F是平面内的一点,若要使以点O、B、E、F为顶点的四边形是菱形,请直接写出点F的坐标.

(1)把(2,1)和(6,-5)两点坐标代入得
,
解这个方程组,得
,
故抛物线的解析式为y=-
x2+
x-2;
(2)令y=0,得-
x2+
x-2=0.
解这个方程,得x1=1,x2=4.
∴A(1,0),B(4,0).
令x=0,得y=-2.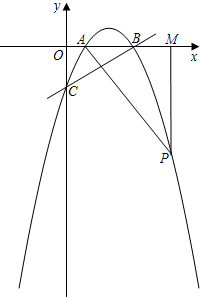
∴C(0,-2).
设P(m,-
m2+
m-2).
因为∠COB=∠AMP=90°,
①当
=
时,△OCB∽△MAP.
∴
=
.
解这个方程,得m1=8,m2=1(舍).
∴点P的坐标为(8,-14).
②当
=
时,△OCB∽△MPA.
∴
=
.
解这个方程,得m1=5,m2=1(舍).
∴点P的坐标为(5,-2).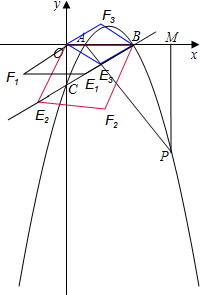
∴点P的坐标为(8,-14)或(5,-2);
(3)点E是直线BC上的一点,点F是平面内的一点,若要使以点O、B、E、F为顶点的四边形是菱形,则以OB,BE,EF为对角线作出来图形,可得到4个菱形;得出点F的坐标为(
,
)或(-
,-
)或(
,-
)或(2,1).
|
解这个方程组,得
|
故抛物线的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)令y=0,得-
| 1 |
| 2 |
| 5 |
| 2 |
解这个方程,得x1=1,x2=4.
∴A(1,0),B(4,0).
令x=0,得y=-2.

∴C(0,-2).
设P(m,-
| 1 |
| 2 |
| 5 |
| 2 |
因为∠COB=∠AMP=90°,
①当
| OC |
| MA |
| OB |
| MP |
∴
| 2 |
| m-1 |
| 4 | ||||
|
解这个方程,得m1=8,m2=1(舍).
∴点P的坐标为(8,-14).
②当
| OC |
| MP |
| OB |
| MA |
∴
| 2 | ||||
|
| 4 |
| m-1 |
解这个方程,得m1=5,m2=1(舍).
∴点P的坐标为(5,-2).

∴点P的坐标为(8,-14)或(5,-2);
(3)点E是直线BC上的一点,点F是平面内的一点,若要使以点O、B、E、F为顶点的四边形是菱形,则以OB,BE,EF为对角线作出来图形,可得到4个菱形;得出点F的坐标为(
| 8 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
| 8 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
| 8 |
| 5 |
| 16 |
| 5 |

练习册系列答案
相关题目