题目内容
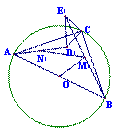
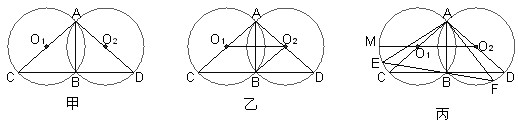
如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.
(1)问B、C、E三点在一条直线上吗?为什么?
(2)若M是线段BE的中点,N是线段AD的中点,试求![]() 的值;
的值;
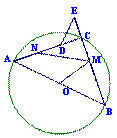
(3)将△DCE绕点C逆时针旋转α(O°<α<90°)后,记为△D![]() CE
CE![]() (图乙),若M
(图乙),若M![]() 是线段BE
是线段BE![]() 的中点,N
的中点,N![]() 是线段AD
是线段AD![]() 的中点,则
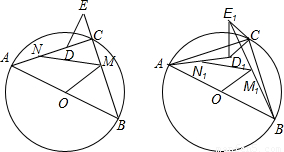
的中点,则![]() =____
=____
(1)解:在一条直线上. ……1分
理由如下:
∵AB为⊙O直径
∴∠ACB=90° ……2分
∵△DCE为等腰直角三角形
∴∠ACE=90°
∴∠BCE=90°+90°=180°
∴B、C、E三点共线. ……3分
(2)连接BD,AE,ON.
∵∠ACB=90°,∠ABC=45°
∴BC=AC
∵DC=DE
∠ACB=∠ACE=90°
 ∴△BCD≌△ACE ……4分
∴△BCD≌△ACE ……4分
∴AE=BD,∠DBE=∠EAC
∴∠DBE+∠BEA=90°
∴BD⊥AE ……5分
∵O,N为中点
∴ON∥BD,ON=![]() BD ……6分
BD ……6分
同理:OM∥AE,OM=![]() AE
AE
∴OM⊥ON,OM=ON ……7分
∴MN=![]() OM
OM
∴![]() =
=![]() ……8分
……8分
(3)![]() ……10分
……10分

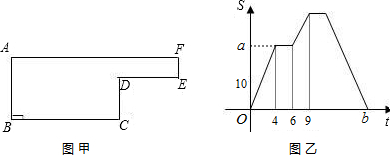 移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:
移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题: 如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.
如图甲,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角△DCE中,∠DCE是直角,点D在线段AC上.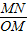 的值;
的值;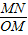 =______
=______
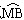 上任取一点E(点E与点B不重合),EB的延长线交优弧
上任取一点E(点E与点B不重合),EB的延长线交优弧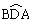 于点F,如图丙所示,连接AE、AF,则AE______AB(请在横线上填上“≥、≤、<、>”这四个不等号中的一个)并加以证明。
于点F,如图丙所示,连接AE、AF,则AE______AB(请在横线上填上“≥、≤、<、>”这四个不等号中的一个)并加以证明。