题目内容
问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中的一些物体进行了测量,下面是他们通过测量得到的一些信息:
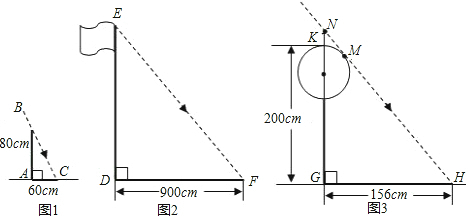
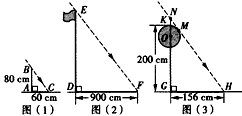
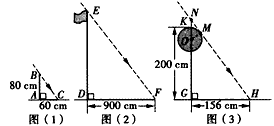
甲组:如图(1),测得一根直立于平地,长为80cm的竹竿的影长为60cm;
乙组:如图(2),测得学校旗杆的影长为900cm;
丙组:如图(3),测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm;
务要求:
甲组:如图(1),测得一根直立于平地,长为80cm的竹竿的影长为60cm;
乙组:如图(2),测得学校旗杆的影长为900cm;
丙组:如图(3),测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm;
务要求:
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图(3),设太阳光线NH与⊙O相切于点M,请根据甲、丙两组得到的信息,求景灯灯罩的半径。
(友情提示:如图(3),景灯的影长等于线段NG的影长;需要时可采用等式:1562+2082=2602)。
(2)如图(3),设太阳光线NH与⊙O相切于点M,请根据甲、丙两组得到的信息,求景灯灯罩的半径。
(友情提示:如图(3),景灯的影长等于线段NG的影长;需要时可采用等式:1562+2082=2602)。
| 解:(1)如图(1)、(2), 由题意可知: ∠BAC=∠EDF=90°,∠BCA=∠EFD, ∴△ABC∽△DEF, ∴ 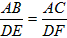 ,即 ,即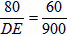 , ,∴DE=1200(cm), ∴学校旗杆的高度是12m; (2)与(1)类似得: 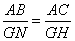 , ,即 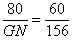 , ,∴GN=208, 在Rt△NGH中,根据勾股定理得: NH2=1562+2082=2602, ∴NH=260, 设⊙O的半径为rcm,连接OM,如图(3) ∵NH切⊙O于M, ∴OM⊥NH, 则∠OMN=∠HGN=90°, 又∠ONM=∠HNG, ∴△OMN∽△HGN, ∴ 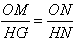 , ,又ON=OK+KN=OK+(GN-GK)=r+8, ∴  ,解得:r=12, ,解得:r=12,∴景灯灯罩的半径是12cm。 |
 |

练习册系列答案
相关题目