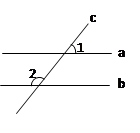题目内容
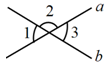
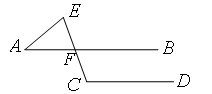
如图,已知 ,
, ,
, 平分
平分 .求证:
.求证: 边平分
边平分 .
.
 ,
, ,
, 平分
平分 .求证:
.求证: 边平分
边平分 .
.见解析
∵∠1十∠2=180°,∠1+∠EBD=180°,
∴∠2=∠EBD,
∴AE∥CF,
又∵∠BAD=∠BCD,
∴∠BCD=∠ADF,
∴AD∥BC,
∴∠DBC=∠BDA= ∠FDB=
∠FDB= ∠DBE,
∠DBE,
∴BC平分∠DBE.
由已知易得∠1=∠BDC,则AE∥CF,所以∠EBC=∠BCD,又∠BAD=∠BCD,故∠EBC=∠BAD,可得AD∥BC,再用角平分线的定义和平行线的性质求证即可.
∴∠2=∠EBD,
∴AE∥CF,
又∵∠BAD=∠BCD,
∴∠BCD=∠ADF,
∴AD∥BC,
∴∠DBC=∠BDA=
 ∠FDB=
∠FDB= ∠DBE,
∠DBE,∴BC平分∠DBE.
由已知易得∠1=∠BDC,则AE∥CF,所以∠EBC=∠BCD,又∠BAD=∠BCD,故∠EBC=∠BAD,可得AD∥BC,再用角平分线的定义和平行线的性质求证即可.

练习册系列答案
相关题目
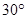
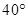


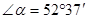 ,则它的补角等于________.
,则它的补角等于________.  、
、 交于点
交于点 ,
, 平分
平分 ,若
,若 ,
, 的度数.
的度数.
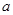 、
、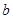 相交,
相交,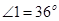 ,则
,则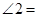 .
.