题目内容
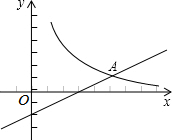 (2013•平凉)如图,一次函数y=
(2013•平凉)如图,一次函数y=| 1 |
| 2 |
| m |
| x |
(1)求反比例函数的解析式;
(2)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
分析:(1)一次函数是完整的函数,把点A的纵坐标代入即可求得M的坐标;然后把A的坐标代入反比例函数解析式,即可求得反比例函数的解析式;
(2)根据交点A的坐标,即可得到当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
(2)根据交点A的坐标,即可得到当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
解答:解:(1)点A在y=
x-2上,
∴1=
x-2,
解得x=6,
把(6,1)代入y=
得
m=6×1=6.
∴y=
;
(2)由图象得,当x>6时,一次函数的值大于反比例函数的值.
| 1 |
| 2 |
∴1=
| 1 |
| 2 |
解得x=6,
把(6,1)代入y=
| m |
| x |
m=6×1=6.
∴y=
| 6 |
| x |
(2)由图象得,当x>6时,一次函数的值大于反比例函数的值.
点评:本题考查用待定系数法求函数解析式;注意:无论是求自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;同时要注意反比例函数的自变量不能取0.

练习册系列答案
相关题目
 (2013•平凉)如图是两个相同的正方体和一个圆锥形组成的立体图形,其主视图是( )
(2013•平凉)如图是两个相同的正方体和一个圆锥形组成的立体图形,其主视图是( ) (2013•平凉)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
(2013•平凉)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )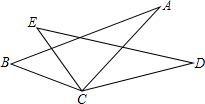 (2013•平凉)如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为
(2013•平凉)如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为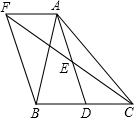 (2013•平凉)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(2013•平凉)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.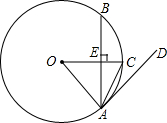 (2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.
(2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.