题目内容
已知:在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD,AD=3cm,BC=7cm.则梯形的高是分析:作AE∥BD交CB的延长线于点E,构建平行四边形,利用已知条件,求出高的长.
解答: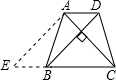 解:如图:
解:如图:
过点A作AE∥BD交CB的延长线于点E
∵AD∥BC
∴四边形AEBD为平行四边形
∴AD=BE=3cm,AE=BD
∵AC⊥BD
∴AE⊥AC
∵等腰梯形ABCD中
∴AC=BD
∴AE=AC
∴梯形的高是Rt△AEC的中线
∴梯形的高是:
EC=
(EB+BC)=5cm.
 解:如图:
解:如图:过点A作AE∥BD交CB的延长线于点E
∵AD∥BC
∴四边形AEBD为平行四边形
∴AD=BE=3cm,AE=BD
∵AC⊥BD
∴AE⊥AC
∵等腰梯形ABCD中
∴AC=BD
∴AE=AC
∴梯形的高是Rt△AEC的中线
∴梯形的高是:
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了等腰梯形的性质,等腰梯形的对角线相等;此题还考查了等腰三角形与直角三角形的性质,解题时要注意辅助线的作法.

练习册系列答案
相关题目
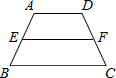 已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )
已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )| A、24 | B、22 | C、20 | D、16 |
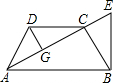 如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
 4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( )
4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( ) (2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )
(2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )