题目内容

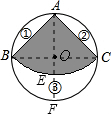
(1)在半径为10的圆的铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积?
(2)若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径?
(3)能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
分析:(1)连接BC,易得AB的长,利用扇形的面积公式可得最大直角扇形的面积;
(2)易得扇形的弧长,除以2π即为圆锥底面圆的半径;
(3)算出余料中能取得圆的最大直径,进而求得最大半径,与(2)中圆锥的底面半径比较,看是否符合即可.
(2)易得扇形的弧长,除以2π即为圆锥底面圆的半径;
(3)算出余料中能取得圆的最大直径,进而求得最大半径,与(2)中圆锥的底面半径比较,看是否符合即可.
解答:解:(1)连接BC,则BC=20,
∵∠BAC=90°,AB=AC,
∴AB=AC=10
,
∴S扇形=
=50π------(2分)
(2)圆锥侧面展开图的弧长为:
=5
,
∴r=
------(3分)
(3)延长AO交⊙O于点F,交扇形于点E,EF=20-10
,最大半径为10-5
<r,
∴不能------(3分)

∵∠BAC=90°,AB=AC,
∴AB=AC=10
| 2 |
∴S扇形=
90π×(10
| ||
| 360 |
(2)圆锥侧面展开图的弧长为:
90π×10
| ||
| 180 |
| 2 |
∴r=
| 5 |
| 2 |
| 2 |
(3)延长AO交⊙O于点F,交扇形于点E,EF=20-10
| 2 |
| 2 |
∴不能------(3分)
点评:考查圆锥的计算;用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长.

练习册系列答案
相关题目
 如图,在半径为10的⊙O中,如果弦心距OC=6,那么弦AB的长等于( )
如图,在半径为10的⊙O中,如果弦心距OC=6,那么弦AB的长等于( )| A、4 | B、8 | C、16 | D、32 |
 如图,在半径为10的⊙O中,OC垂直弦AB于点D,AB=16,则CD的长是
如图,在半径为10的⊙O中,OC垂直弦AB于点D,AB=16,则CD的长是