题目内容
求一次函数y=x-4和y=-x-4与x轴围成三角形的面积．分析：根据两个函数方程联立解得交点坐标，再利用面积公式进行求解．
解答：解：y=x-4与y=-x-4联立解得交点坐标为（0，-4），
y=x-4与x轴的交点是（4，0），
y=-x-4与x轴的交点是（-4，0），
故围成三角形的面积为：
×(4+4)× 4=16．
y=x-4与x轴的交点是（4，0），
y=-x-4与x轴的交点是（-4，0），
故围成三角形的面积为：
| 1 |
| 2 |
点评：本题考查了三角形面积公式以及根据公式代入数值解题的能力．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
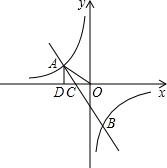于D，若OA=
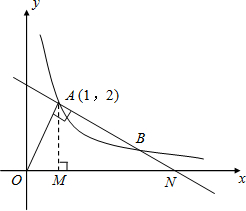如图，一次函数y=kx+b图象与反比例函数y=
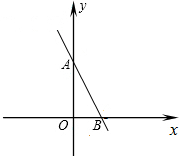如图，一次函数y=kx+b图象经过点（1，2）、点（-1，6），分别与y轴、x轴交于A．B两点．