题目内容
如图所示，E是正方形ABCD的边AB上的动点， EF⊥DE交BC于点F．
（1）求证: 
ADE∽BEF；
（2） 设正方形的边长为4， AE=
，BF=
．当取什么值时，有最大值?并求出这个最大值．
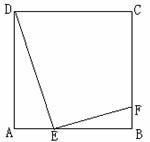
证明：（1）因为ABCD是正方形，所以
∠DAE=∠FBE=
，
所以∠ADE+∠DEA=，
又EF⊥DE，所以∠AED+∠FEB=，
所以∠ADE=∠FEB，
所以
ADE∽BEF．
（2）解：由（1） ADE∽BEF，AD=4，BE=4-
，得
，得
=
=
，
所以当=2时， 有最大值，
的最大值为1．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
23、如图所示，E是正方形ABCD的边CD上一点，将△AED绕点A顺时针旋转90°，得到△AFB，则AE与AF有何关系？试说明理由．
18、如图所示，ABCD是正方形，BE⊥BF，BE=BF，试判断AE与FC的位置关系，并给出证明．
如图所示，E是正方形ABCD的边BC延长线上的点，且BC=CE．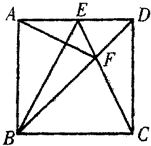
23、如图所示，E是正方形ABCD中AD边上的中点，BD与CE交于点F．请你根据图形判断AF与BE的位置具有什么关系？并给予证明．
如图所示，P是正方形ABCD的边CD上一点，∠BAP的角平分线交BC于Q，