��Ŀ����
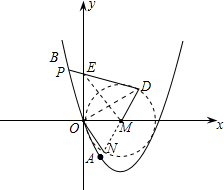 ��֪����ͼ��������y=ax2+bx+c����ԭ�㣨0��0����A��1��-3����B��-1��5�����㣮
��֪����ͼ��������y=ax2+bx+c����ԭ�㣨0��0����A��1��-3����B��-1��5�����㣮��1���������ߵĽ���ʽ��
��2������������x�����һ������ΪC����OCΪֱ������M���������������һ��P����M������PD���е�ΪD����y��������ύ�ڵ�ΪE������MD����֪��E������Ϊ��0��m�������ı���EOMD����������ú�m�Ĵ���ʽ��ʾ��
��3���ӳ�DM����M�ڵ�N������ON��OD������P�ڣ�2�����������˶���ʲôλ��ʱ����ʹ��S�ı���EOMD=S��DON���������ʱ��P�����꣮
��������1����O��A��B����������������ߵĽ���ʽ�У������������ϵ����ֵ���Ӷ�ȷ�������ߵĽ���ʽ��
��2������EM������ED��EO���ǡ�M�����ߣ��������߳������ɵõ�ED=EO������SSS��֤�á�EDM�ա�EOM�������ǵ������ȣ�����ı���EOMD�������ʵ�ǡ�EOM�������2������OMΪ�ף�OEΪ���������EOM����������ɵõ��ı���EOMD���������ʽ��
��3����DON�У�MN=DM�����ԡ�DMO�͡�OMN�ȵ�ͬ�ߣ����ǵ������ȣ��ɴ˿�֤�á�EOM���OMD�������ȣ����������������ι��õױ�OM����ED��x�ᣬ���ݡ�M�İ뾶���õ�ֱ��PD�Ľ���ʽ�����������ߵĽ���ʽ�������P������꣮
��2������EM������ED��EO���ǡ�M�����ߣ��������߳������ɵõ�ED=EO������SSS��֤�á�EDM�ա�EOM�������ǵ������ȣ�����ı���EOMD�������ʵ�ǡ�EOM�������2������OMΪ�ף�OEΪ���������EOM����������ɵõ��ı���EOMD���������ʽ��
��3����DON�У�MN=DM�����ԡ�DMO�͡�OMN�ȵ�ͬ�ߣ����ǵ������ȣ��ɴ˿�֤�á�EOM���OMD�������ȣ����������������ι��õױ�OM����ED��x�ᣬ���ݡ�M�İ뾶���õ�ֱ��PD�Ľ���ʽ�����������ߵĽ���ʽ�������P������꣮
����⣺��1����������y=ax2+bx+c��O��0��0����A��1��-3����B��-1��5�����㣬
��
��
���
��
�������ߵĽ���ʽΪy=x2-4x��
��2��������y=x2-4x�������һ����������ΪC��4��0����
����EM��
���M�İ뾶��2����OM=DM=2��
��ED��EO���ǡ�M�����ߣ�
��EO=ED��
���EOM�ա�EDM��
��S�ı���EOMD=2S��OME=2��
OM•OE=2m��
��3�����D��������x0��y0����
��S��DON=2S��DOM=2��
OM��y0=2y0��
��S�ı���EOMD=S��DONʱ����2m=2y0��m=y0��
��m=y0��ED��x�ᣬ
�֡�EDΪ���ߣ�
��D���������2��2����
��P��ֱ��ED�ϣ�����P�������Ϊ��x��2����
��P���������ϣ�
��2=x2-4x��
���x=2��
��
��P��2+
��2����P��2-
��2������
��
|
���
|
�������ߵĽ���ʽΪy=x2-4x��
��2��������y=x2-4x�������һ����������ΪC��4��0����
����EM��
���M�İ뾶��2����OM=DM=2��
��ED��EO���ǡ�M�����ߣ�
��EO=ED��
���EOM�ա�EDM��
��S�ı���EOMD=2S��OME=2��
| 1 |
| 2 |
��3�����D��������x0��y0����
��S��DON=2S��DOM=2��
| 1 |
| 2 |
��S�ı���EOMD=S��DONʱ����2m=2y0��m=y0��
��m=y0��ED��x�ᣬ
�֡�EDΪ���ߣ�
��D���������2��2����
��P��ֱ��ED�ϣ�����P�������Ϊ��x��2����
��P���������ϣ�
��2=x2-4x��
���x=2��
| 6 |
��P��2+
| 6 |
| 6 |
�����������Ƕ��κ�����Բ���ۺ��⣬�����˶��κ�������ʽ��ȷ����ȫ�������ε����ʡ����߳�����������ͼ�㼰ͼ�����������Ҫ֪ʶ�������ѶȽϴ�ע���ܹ����֡�EOM����OMD�������ϵ���Ӷ��õ�ֱ��PD��x���λ�ù�ϵ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д�
�����Ŀ
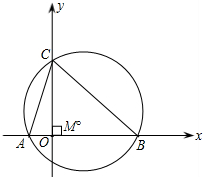 ��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M��
��y�ύ��C��������Ϊ3����ABC�����Բ��Բ��Ϊ��M�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��
��2013•�������ʼ죩��֪����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A�� ��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0����
��֪����ͼ��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0���� ��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�
��֪����ͼ��������y=x2+px+q��x���ཻ��A��B���㣬��y�ύ�ڵ�C����OA��OB��OA=OC���������ߵĶ���Ϊ��P��ֱ��PC��x��Ľ���Dǡ�����A����y��Գƣ�