题目内容
如图,△ABC中,∠ACB=90°,AC=BC.D是AC上一点,且AD=2CD,CE⊥BD于H交AB于E.F是AB的中点,BD、CF交于点G,连接EG.下列结论:①BG=CE;②四边形AEGC为等腰梯形;③HG=2HD;④BE=3AE.其中正确的结论有( )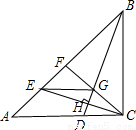
A.4个
B.3个
C.2个
D.1个
【答案】分析:由点F是AB中点,AC=BC,∠ACB=90°,CF⊥AB,∠FCB=∠BAC=45°,在△ACE中∥∥,∠CEA=90°+∠ECF,在△BGC中∠CGB=90°+∠ECF,∠CEA=∠CGB,又AC=BC,所以△AEC≌△BCG即得证①;由AE=CG,作FM∥AC,则AD=2CD,所以FG=GC,得AE=CG,AE=EF,又得EG∥AC,所以四边形AEGC为等腰梯形(②得证)所以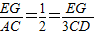 即
即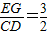 ,得
,得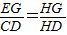 =
= ③是错误的;由
③是错误的;由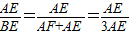 =
= (④得证).
(④得证).
解答: 解:∵点F是AB中点,AC=BC,∠ACB=90°
解:∵点F是AB中点,AC=BC,∠ACB=90°
∴CF⊥AB,∠FCB=∠BAC=45°
在△ACE中,∠CEA=90°+∠ECF,在△BGC中∠CGB=90°+∠ECF
∴∠CEA=∠CGB
又∵AC=BC
∴△AEC≌△BCG
∴AE=CG,BG=CE(①得证)
由AE=CG,
作FM∥AC
∵AD=2CD,
∴FG=GC,
∴AE=CG,AE=EF,
∴EG∥AC
∴四边形AEGC为等腰梯形(②得证)
∴ 即
即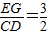
∴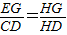 =
=
∴③是错误的.
由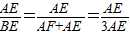 =
= (④得证)
(④得证)
故选B.
点评:本题考查了等腰直角三角形,综合考查了平行线的与线段的巧妙结合,本题思路性很强.
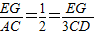 即
即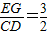 ,得
,得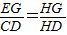 =
= ③是错误的;由
③是错误的;由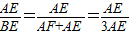 =
= (④得证).
(④得证).解答:
 解:∵点F是AB中点,AC=BC,∠ACB=90°
解:∵点F是AB中点,AC=BC,∠ACB=90°∴CF⊥AB,∠FCB=∠BAC=45°
在△ACE中,∠CEA=90°+∠ECF,在△BGC中∠CGB=90°+∠ECF
∴∠CEA=∠CGB
又∵AC=BC
∴△AEC≌△BCG
∴AE=CG,BG=CE(①得证)
由AE=CG,
作FM∥AC
∵AD=2CD,
∴FG=GC,
∴AE=CG,AE=EF,
∴EG∥AC
∴四边形AEGC为等腰梯形(②得证)
∴
 即
即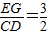
∴
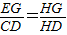 =
=
∴③是错误的.
由
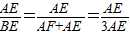 =
= (④得证)
(④得证)故选B.
点评:本题考查了等腰直角三角形,综合考查了平行线的与线段的巧妙结合,本题思路性很强.

练习册系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.