题目内容
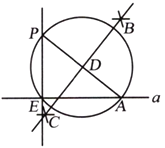
【题目】如图,⊙O是△ABC的外接圆,AB是直径,OD⊥AC,垂足为D点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PB,PC,且满足∠PCA=∠ABC
(1)求证:PA=PC;
(2)求证:PA是⊙O的切线;
(3)若BC=8,![]() ,求DE的长.
,求DE的长.
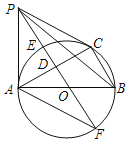
【答案】(1)详见解析;(2)详见解析;(3)DE=8.
【解析】
(1)根据垂径定理可得AD=CD,得PD是AC的垂直平分线,可判断出PA=PC;
(2)由PC=PA得出∠PAC=∠PCA,再判断出∠ACB=90°,得出∠CAB+∠CBA=90°,再判断出∠PCA+∠CAB=90°,得出∠CAB+∠PAC=90°,即可得出结论;
(2)根据AB和DF的比设AB=3a,DF=2a,先根据三角形中位线可得OD=4,从而得结论.
(1)证明∵OD⊥AC,
∴AD=CD,
∴PD是AC的垂直平分线,
∴PA=PC,
(2)证明:由(1)知:PA=PC,
∴∠PAC=∠PCA.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°.
又∵∠PCA=∠ABC,
∴∠PCA+∠CAB=90°,
∴∠CAB+∠PAC=90°,即AB⊥PA,
∴PA是⊙O的切线;
(3)解:∵AD=CD,OA=OB,
∴OD∥BC,OD=![]() BC=
BC=![]() =4,
=4,
∵![]() ,
,
设AB=3a,DF=2a,
∵AB=EF,
∴DE=3a﹣2a=a,
∴OD=4=![]() ﹣a,
﹣a,
a=8,
∴DE=8.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案【题目】东坡商贸公司购进某种水果成本为20元/![]() ,经过市场调研发现,这种水果在未来48天的销售单价
,经过市场调研发现,这种水果在未来48天的销售单价![]() (元/
(元/![]() )与时间
)与时间![]() (天)之间的函数关系式
(天)之间的函数关系式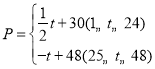 ,
,![]() 为整数,且其日销售量
为整数,且其日销售量![]() (
(![]() )与时间
)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | … |
日销售量 | 118 | 114 | 108 | 100 | 80 | … |
(1)已知![]() 与
与![]() 之间的变化符合一次函数关系,试求在第30天的日销售量;
之间的变化符合一次函数关系,试求在第30天的日销售量;
(2)哪一天的销售利润最大?最大日销售利润为多少?
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?