Question

【题目】一个圆形喷水池的中心竖立一根高为顶端装有喷头的水管，喷头喷出的水柱呈抛物线形．当水柱与池中心的水平距离为时，水柱达到最高处，高度为．

求水柱落地处与池中心的距离；

如果要将水柱的最大高度再增加，水柱的最高处与池中心的水平距离以及落地处与池中心的距离仍保持不变，那么水管的高度应是多少？

Answer 1

【答案】水柱落地处与池中心的距离为；水管的高度应为．

【解析】

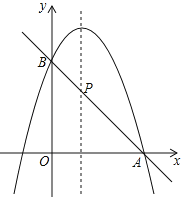
首先根据题意建立直角坐标系,画出拋物线、(1)结合图形我们可以知道此拋物线的顶点坐标(1,3),而且抛物线经过点(0,2.25),求出抛物线的解析式,把(x,0)代入解析式即可解题,

(2)由(1)的结论我们知道了水柱落地的坐标为(3,0),顶点坐标为(1,4),求出新的拋物线的解析式,再求水管的高度即可解题.

如图，建立直角坐标系，点是抛物线的顶点．

由题意，设水柱所在的抛物线的解析式为，

∵抛物线经过点，

∴，即，

∴，

当时，即，

解得或（舍），

即水柱落地处与池中心的距离为；

由题意，设抛物线解析式为，

∵抛物线经过点，

∴，即，

∴，

当时，，

即水管的高度应为．