题目内容
某工厂用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方体纸盒.设加工竖式纸盒x个,横式纸盒y个.
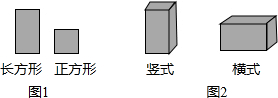
(1)根据题意,完成以下表格:
(2)工人李娟从仓库领来了长方形纸板2012张,正方形纸板1003张,请你帮她计划竖式纸盒、横式纸盒各加工多少个,恰好将领来的纸板全部用完;
(3)李娟有一张领取材料的清单,上面写着:长方形纸板a张(碰巧a处的数字看不清了,她只记得不超过142张),正方形纸板90张.并且领来的材料恰好全部用于加工上述两种纸盒,试求出她加工这两种盒子各多少个?

(1)根据题意,完成以下表格:
| 纸盒 纸板 |
竖式纸盒(个) | 横式纸盒(个) |
| x | y | |
| 长方形纸板(张) | 4x 4x |
3y |
| 正方形纸板(张) | x | 2y 2y |
(3)李娟有一张领取材料的清单,上面写着:长方形纸板a张(碰巧a处的数字看不清了,她只记得不超过142张),正方形纸板90张.并且领来的材料恰好全部用于加工上述两种纸盒,试求出她加工这两种盒子各多少个?
分析:(1)结合题意,根据无盖的长方体纸盒的组成特征结合图形便可得出答案;
(2)可根据长方形纸板2012张,正方形纸板1003张为等量关系建立二元一次方程组,求出其解即可;
(3)设做竖式纸盒x个,横式纸盒y个,列出二元一次方程组,解方程组得到关于y的不等式,根据题中给出的a的取值范围便可求出y的取值范围,进而求出x的值.
(2)可根据长方形纸板2012张,正方形纸板1003张为等量关系建立二元一次方程组,求出其解即可;
(3)设做竖式纸盒x个,横式纸盒y个,列出二元一次方程组,解方程组得到关于y的不等式,根据题中给出的a的取值范围便可求出y的取值范围,进而求出x的值.
解答:解:(1)完成表格如下所示:
(2)由题意得:
,
解得:
,
答:竖式纸盒加工203个,横式纸盒加工400个.
(3)由题意得:
,
解得y=72-
a,x=90-2y,
∵a≤142,
∴y≥43.6,
∵x>0,
∴90-2y>0,
∴y<45,
∴43.6≤y<45,
∵y为正整数,
∴y=44,x=2,
答:他做竖式纸盒2个,横式纸盒44个.
| 纸盒 纸板 |
竖式纸盒(个) | 横式纸盒(个) |
| x | y | |
| 长方形纸板(张) | 4x | 3y |
| 正方形纸板(张) | x | 2y |
|
解得:
|
答:竖式纸盒加工203个,横式纸盒加工400个.
(3)由题意得:
|
解得y=72-
| 1 |
| 5 |
∵a≤142,
∴y≥43.6,
∵x>0,
∴90-2y>0,
∴y<45,
∴43.6≤y<45,
∵y为正整数,
∴y=44,x=2,
答:他做竖式纸盒2个,横式纸盒44个.
点评:本题考查一元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题根据竖式及横式的组成得出方程求解.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种无盖的长方体纸盒.(长方形的宽与正方形的边长相等)
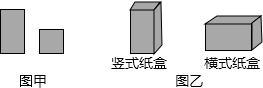
(1)现有正方形纸板50张,长方形纸板100张,若要做竖式纸盒个x,横式纸盒y个.
①根据题意,完成以下表格:
②若纸板全部用完,求x、y的值;
(2)若有正方形纸板90张,长方形纸板a张(a是整数),做成上述两种纸盒,纸板恰好全部用完.已知164<a<174,求a的值.

(1)现有正方形纸板50张,长方形纸板100张,若要做竖式纸盒个x,横式纸盒y个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | |
| 长方形纸板(张) | 3y |
(2)若有正方形纸板90张,长方形纸板a张(a是整数),做成上述两种纸盒,纸板恰好全部用完.已知164<a<174,求a的值.
某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒 .
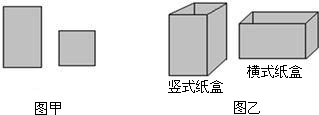
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
②按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.

(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
纸盒 纸板 |
竖式纸盒(个) | 横式纸盒(个) |
| x | 100-x | |
| 正方形纸板(张) | 2(100-x) | |
| 长方形纸板(张) | 4x |
(2)若有正方形纸162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.
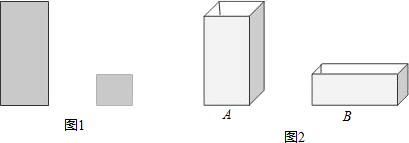
 (2012•新疆)某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?
(2012•新疆)某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?