题目内容
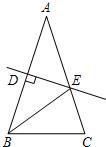 2、如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
2、如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )分析:要求△BEC的周长,现有BC=5,只要求得CE+BE即可,根据线段垂直平分线的性质得BE=AE,于是只要得到AC问题可解,由已知条件结合等腰三角形的周长不难求出AC的大小,答案可得.
解答:解:△ABC为等腰三角形,
所以AB=AC,
因为BC=5,
所以2AB=2AC=21-5=16,
即AB=AC=8,
而DE是线段AB的垂直平分线,
∴BE=AE,故BE+EC=AE+EC=AC=8
∴△BEC的周长=BC+BE+EC=5+8=13.
故选A.
所以AB=AC,
因为BC=5,
所以2AB=2AC=21-5=16,
即AB=AC=8,
而DE是线段AB的垂直平分线,
∴BE=AE,故BE+EC=AE+EC=AC=8
∴△BEC的周长=BC+BE+EC=5+8=13.
故选A.
点评:本题考查线段垂直平方线的性质及等腰三角形的性质.由题中DE是线段AB的垂直平分线这一条件时,一般要用到它的性质定理:线段垂直平分线上的点到线段两端的距离相等.从而结合图形找到这对相等的线段是解决问题的关键.

练习册系列答案
相关题目
 已知:如图,等腰△ABC的腰长为2
已知:如图,等腰△ABC的腰长为2 如图,等腰△ABC的底边BC为16,底边上的高AD为6,则腰长AB的长为
如图,等腰△ABC的底边BC为16,底边上的高AD为6,则腰长AB的长为 如图,等腰△ABC的腰长是5cm,底边长是6cm,P是底边BC上任意一点,PD⊥AB,PE⊥AC,垂足分别是D,E,那么PD+PE=
如图,等腰△ABC的腰长是5cm,底边长是6cm,P是底边BC上任意一点,PD⊥AB,PE⊥AC,垂足分别是D,E,那么PD+PE=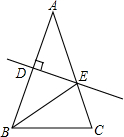 如图,等腰△ABC的周长为27,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC的周长为27,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( ) 如图,等腰△ABC的顶角为120°,腰长为10,则底边BC上的中线AD长为
如图,等腰△ABC的顶角为120°,腰长为10,则底边BC上的中线AD长为