题目内容
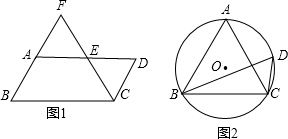 (1)如图1,在?ABCD中,点E是AD的中点,连接CE并延长,交BA的延长线于点F.求证:FA=AB.
(1)如图1,在?ABCD中,点E是AD的中点,连接CE并延长,交BA的延长线于点F.求证:FA=AB.(2)如图2,在⊙O中,∠ACB=∠BDC=60°,AC=2
| 2 |
分析:(1)由ABCD为平行四边形,得到对边平行且相等,由FB与CD平行,利用两直线平行内错角相等得到两对内错角相等,又E为AD的中点,得到AE=DE,利用AAS可得三角形AEF与三角形ECD全等,根据全等三角形的对应边相等可得AF=DC,又AB=DC,等量代换可得FA=AB;
(2)由同弧所对的圆周角相等可得∠BDC=∠BAC,由∠BDC的度数求出∠BAC的度数,可得∠ACB与∠BAC的度数相等,都为60°,可得三角形ABC为等边三角形,由O为三角形的外心,可得O为三边垂直平分线的交点,根据三线合一得到的O为三内角角平分线的交点,连接AO并延长交BC与M,连接OC,在直角三角形OMC中,根据30°角所对的直角边等于斜边的一半,可得OC=2OM,又OA=OC,可得AO=2OM,表示出OM,在直角三角形ACM中,利用勾股定理求出AM的长,由AM=AO+OM,把表示出OM代入,得到关于OA的方程,求出方程的解得到OA的长,即为圆的半径,即可求出圆的周长.
(2)由同弧所对的圆周角相等可得∠BDC=∠BAC,由∠BDC的度数求出∠BAC的度数,可得∠ACB与∠BAC的度数相等,都为60°,可得三角形ABC为等边三角形,由O为三角形的外心,可得O为三边垂直平分线的交点,根据三线合一得到的O为三内角角平分线的交点,连接AO并延长交BC与M,连接OC,在直角三角形OMC中,根据30°角所对的直角边等于斜边的一半,可得OC=2OM,又OA=OC,可得AO=2OM,表示出OM,在直角三角形ACM中,利用勾股定理求出AM的长,由AM=AO+OM,把表示出OM代入,得到关于OA的方程,求出方程的解得到OA的长,即为圆的半径,即可求出圆的周长.
解答:解:(1)∵ABCD为平行四边形,
∴FB∥DC,AB=CD,
∴∠F=∠DCE,∠FAE=∠D,
又E为AD的中点,∴AE=DE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴FA=CD,
∴FA=AB;

(2)∵圆周角∠BAC与∠BDC所对的弧都为
,
∴∠BAC=∠BDC,又∠BDC=60°,
∴∠BAC=60°;
连接AO,并延长与BC交于M,连接OC,
则AM⊥BC,
∵∠ACB=∠BAC=60°,∴∠ABC=60°,
∴△ABC为等边三角形,又AC=2
cm,
∴M为BC的中点,即CM=BM=
BC=
cm,CO为∠ACB的平分线,即∠MCO=∠AOC=30°,
在Rt△AMC中,根据勾股定理得:AM=
=
cm,
在Rt△MOC中,OM=
OC,又OA=OC,
∴OM=
OA,
∴AM=OA+OM=OA+
OA=
OA=
cm,
可得:OA=
cm,
则圆O的周长为2πr=
cm.
∴FB∥DC,AB=CD,
∴∠F=∠DCE,∠FAE=∠D,
又E为AD的中点,∴AE=DE,
在△AEF和△DEC中,
|
∴△AEF≌△DEC(AAS),
∴FA=CD,
∴FA=AB;

(2)∵圆周角∠BAC与∠BDC所对的弧都为
 |
| BC |
∴∠BAC=∠BDC,又∠BDC=60°,
∴∠BAC=60°;
连接AO,并延长与BC交于M,连接OC,
则AM⊥BC,
∵∠ACB=∠BAC=60°,∴∠ABC=60°,
∴△ABC为等边三角形,又AC=2
| 2 |
∴M为BC的中点,即CM=BM=
| 1 |
| 2 |
| 2 |
在Rt△AMC中,根据勾股定理得:AM=
| AC2-CM2 |
| 6 |
在Rt△MOC中,OM=
| 1 |
| 2 |
∴OM=
| 1 |
| 2 |
∴AM=OA+OM=OA+
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
可得:OA=
2
| ||
| 3 |
则圆O的周长为2πr=
4π
| ||
| 3 |
点评:此题考查了圆周角定理,平行四边形的性质,全等三角形的判定与性质,等边三角形的判定与性质,含30°角直角三角形的性质,以及勾股定理,根据题意判定出△ABC为等边三角形是解第二问的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目



 图2,中间会出现一个小孔,如果正方形ABCD的边长为a,试计算图2中小孔的面积.
图2,中间会出现一个小孔,如果正方形ABCD的边长为a,试计算图2中小孔的面积.