Question

【题目】如图，抛物线y＝（x﹣1）2﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，经过点C作x轴的平行线，与抛物线的另一个交点为点D，M为抛物线的顶点，P（m，n）是抛物线上点A，C之间的一点（不与点A，C重合），以下结论：①OC＝4；②点D的坐标为（2，﹣3）；③n+3＞0；④存在点P，使PM⊥DM．其中正确的是（　　）

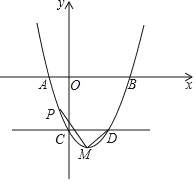
A. ①③ B. ②③ C. ②④ D. ①④

Answer 1

【答案】B

【解析】

利用二次函数的性质一一进行判断可得答案.

解:①将x=0时,y=-3,

c(0,-3),OC=3,故①错误；

②当y=-3时,-3=(x-1)-4,解:x=0或x=2

D(2,-3),故②正确.

③点P在AC之间,且C(0,-3),

.n>-3,n+3>0,故③正确；

④易得M点坐标(1,-4).

MC=DM=

又CD=2

MC+DM=CD,.

∠CMD=90.点 P和点 C重合,

PM不垂直于 DM, 故④错.

故正确为②③，故选B.