题目内容
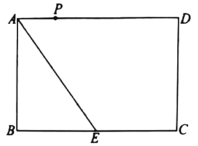
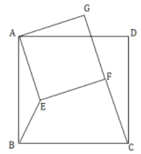
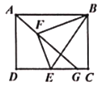
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
A.1B.1.5C.4-![]() D.4-
D.4-![]()
【答案】D
【解析】
由图可知:DG最小时CG最大,故当∠GAD最小(∠GAB最大)时,CG取最大值,由F在以B为圆心,BC为半径的圆上得到AF⊥BF,此时点G、E重合,证明△ABF≌△AED,得到AE=AB=4,再利用勾股定理求出DE即可得到CG的最大值.
由图可知:DG最小时CG最大,故当∠GAD最小(∠GAB最大)时,CG取最大值,
∵F在以B为圆心,BC为半径的圆上,
∴AF与圆相切时,∠GAB最大,
即AF⊥BF,此时点G、E重合,
∵AB∥CD,
∴∠BAF=∠AED,
∵∠AFB=∠D=90°,BF=BC=AD,
∴△ABF≌△AED,
∴AE=AB=4,
∴DE=![]() ,
,
∴CE=CG=![]() ,
,
故选:D.

练习册系列答案
相关题目
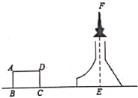
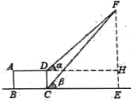
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)