题目内容
若a、b互为相反数,c、d互为倒数,则(a+b)2009+(c·d)2009=_____________
1
分析:首先理解a b互为相反数和c d互为倒数的含义,得到a+b=0,cd=1,代入后利用有理数的乘方的意义计算即可.
解:∵a、b互为相反数,c、d互为倒数,
∴a+b=0,cd=1,
∴(a+b)2009+(cd)2009,
=02009+12009,
=1.
故答案为:若a、b互为相反数,c、d互为倒数,则(a+b)2009+(c?d)2009=1.
点评:解此题的关键是检查对相反数和倒数的理解和掌握.突破点是得到a+b=0,cd=1.题型很好,难度适中.
解:∵a、b互为相反数,c、d互为倒数,
∴a+b=0,cd=1,
∴(a+b)2009+(cd)2009,
=02009+12009,
=1.
故答案为:若a、b互为相反数,c、d互为倒数,则(a+b)2009+(c?d)2009=1.
点评:解此题的关键是检查对相反数和倒数的理解和掌握.突破点是得到a+b=0,cd=1.题型很好,难度适中.

练习册系列答案
相关题目
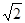 最接近的无理数是 ( )
最接近的无理数是 ( )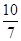
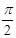
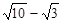

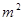 ,将5 280 000用科学记数法表示为
,将5 280 000用科学记数法表示为  的结果是
的结果是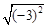 的结果是 .
的结果是 .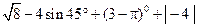 .
.