Question

（2012•攀枝花）据媒体报道，近期“手足口病”可能进入发病高峰期，某校根据《学校卫生工作条例》，为预防“手足口病”，对教室进行“薰药消毒”．已知药物在燃烧及释放过程中，室内空气中每立方米含药量y（毫克）与燃烧时间x（分钟）之间的关系如图所示（即图中线段OA和双曲线在A点及其右侧的部分），根据图象所示信息，解答下列问题：
（1）写出从药物释放开始，y与x之间的函数关系式及自变量的取值范围；
（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？

Answer 1

分析：首先根据题意，药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例；药物释放完毕后，y与x成反比例，将数据代入用待定系数法可得反比例函数的关系式；进一步求解可得答案．

解答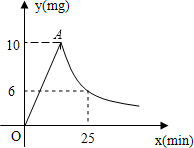：解：（1）设反比例函数解析式为y=

k

x

（k≠0），
将（25，6）代入解析式得，k=25×6=150，
则函数解析式为y=

150

x

（x≥15），
将y=10代入解析式得，10=

150

x

，
x=15，
故A（15，10），
设正比例函数解析式为y=nx，
将A（15，10）代入上式即可求出n的值，
n=

10

15

=

2

3

，
则正比例函数解析式为y=

2

3

x（0≤x＜15）．

（2）当y=2时，x=3．

150

x

=2，
解得x=75，
75-3=72（分钟）
答：从消毒开始，师生至少在72分钟内不能进入教室．

点评：本题考查了反比例函数的应用，现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式．