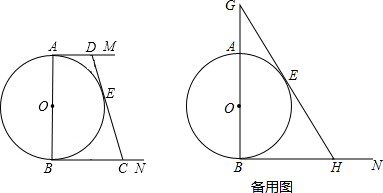
题目内容
如图,直径AB=12cm,AM、BN是⊙O的切线,切点分别为A、B.
(1)若AD=4cm,DC是⊙O的切线,切点为E,求BC的长.
(2)若一只蚂蚁从B点出发沿BA方向走到G点,速度为每秒4cm;同时另一只蚂蚁也从B点出发沿BN方向走到H点,速度为每秒3cm,连接GH,求经过多少秒后,GH与⊙O相切(结果保留根号).
(1)若AD=4cm,DC是⊙O的切线,切点为E,求BC的长.
(2)若一只蚂蚁从B点出发沿BA方向走到G点,速度为每秒4cm;同时另一只蚂蚁也从B点出发沿BN方向走到H点,速度为每秒3cm,连接GH,求经过多少秒后,GH与⊙O相切(结果保留根号).

分析:(1)根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系,即线段BC与已知线段AD间的数量关系;
(2)设经过t秒后,GH与⊙O相切.如备用图,过点A作AD⊥AB交GH于点C,构建相似三角形△GAD∽△GBH,则对应边成比例:
=
,即
=
,①
由(1)知,当GH与⊙O相切时,BH=
,即3t=
②,根据①②即可求得t的值.
(2)设经过t秒后,GH与⊙O相切.如备用图,过点A作AD⊥AB交GH于点C,构建相似三角形△GAD∽△GBH,则对应边成比例:
| GA |
| GB |
| AD |
| BH |
| 4t-12 |
| 4t |
| AD |
| 3t |
由(1)知,当GH与⊙O相切时,BH=
| 36 |
| AD |
| 36 |
| AD |
解答: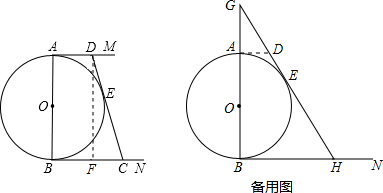 解:作DF⊥BN交BC于F;
解:作DF⊥BN交BC于F;
∵AM、BN与⊙O切于点定A、B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠A=∠B=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BC-BF=y-x;
∵DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(x-y)2+122,
整理为y=
,即BC=
=9(cm),即BC的长度为9cm;
(2)设经过t秒后,GH与⊙O相切.
如备用图,过点A作AD⊥AB交GH于点C.
∵BN是⊙O的切线,
∴BN⊥AB,
∴AD∥BH,
∴△GAD∽△GBH,
∴
=
,即
=
,①
由(1)知,当GH与⊙O相切时,BH=
,即3t=
,②
由①②解得t=4或t=-1(舍去).
所以,当经过4秒后,GH与⊙O相切.
 解:作DF⊥BN交BC于F;
解:作DF⊥BN交BC于F;∵AM、BN与⊙O切于点定A、B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠A=∠B=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BC-BF=y-x;
∵DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(x-y)2+122,
整理为y=
| 36 |
| x |
| 36 |
| 4 |
(2)设经过t秒后,GH与⊙O相切.
如备用图,过点A作AD⊥AB交GH于点C.
∵BN是⊙O的切线,
∴BN⊥AB,
∴AD∥BH,
∴△GAD∽△GBH,
∴
| GA |
| GB |
| AD |
| BH |
| 4t-12 |
| 4t |
| AD |
| 3t |
由(1)知,当GH与⊙O相切时,BH=
| 36 |
| AD |
| 36 |
| AD |
由①②解得t=4或t=-1(舍去).
所以,当经过4秒后,GH与⊙O相切.
点评:本题考查了圆的综合题.其中涉及到了矩形的判定与性质,勾股定理,切线的性质.解答(2)题时,可以直接利用(1)中的函数关系式.

练习册系列答案
相关题目
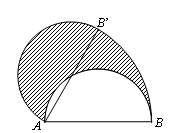
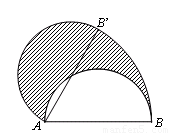
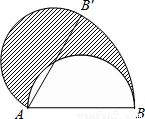
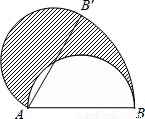
 (2013•新余模拟)如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是
(2013•新余模拟)如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是