题目内容
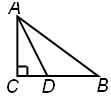
如图:在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,AC=6cm,那么点D到AB的距离是____ ____cm.

3
试题分析:过点D作DE⊥AB于点E,由∠C=90°,AD平分∠CAB再结合公共边AD可证得△ACD≌△AED,根据勾股定理可求得AB的长,从而可以得到BE的长,设CD=DE=x,在Rt△BED中,根据勾股定理列方程求解即可.
过点D作DE⊥AB于点E,

∵AD平分∠CAB
∴∠CAD=∠EAD
∵∠C=∠AED=90°,AD=AD
∴△ACD≌△AED
∴AC=AE=6,CD=DE
∵∠C=90°,BC=8,AC=6
∴

∴BE=ABAE=4
设CD=DE=x,则BD=8x
在Rt△BED中,

即
 ,解得
,解得
∴点D到AB的距离是3cm.

练习册系列答案
相关题目
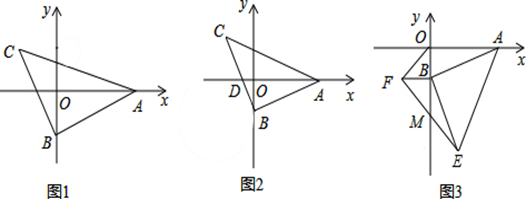
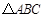 与
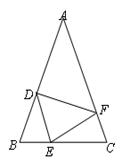
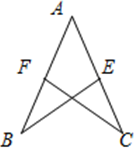
与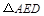 均是等边三角形,连接BE、CD.请在图中找出一条与
均是等边三角形,连接BE、CD.请在图中找出一条与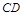 长度相等的线段,并证明你的结论.
长度相等的线段,并证明你的结论.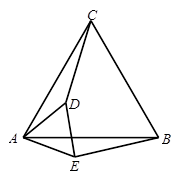
 的周长是21,OB,OC分别平分∠ABC和∠ACB,
的周长是21,OB,OC分别平分∠ABC和∠ACB,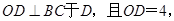 △ABC的面积是_______.
△ABC的面积是_______.