Question

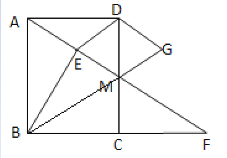
【题目】如图，在矩形ABCD中，∠DAF＝300，M是CD上一点，AM的延长线交BC的延长线于点F，BE垂直平分AM，DG∥AF，MG∥DE．

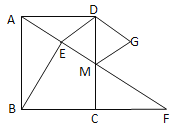
（1）判断四边形DEMG的形状，并说明理由；

（2）求证：△ADM≌△FCM．

Answer 1

【答案】（1）四边形DEMG是菱形，见解析；（2）见解析.

【解析】

（1）先证明四边形DEMG是平行四边形，再根据Rt△ADM斜边上的中线等于斜边的一半，得到邻边相等，故可证明菱形；

（2）连接BM，根据BE垂直平分AM，得到AB＝BM，即可证明△ADM≌△FCM.

（1）四边形DEMG是菱形

∵DG∥AF，MG∥DE

∴四边形DEMG是平行四边形

∵矩形ABCD

∴∠ADC＝900

∵BE平分AM

∴DE＝EM

∴四边形DEMG是菱形

（2）证明：连接BM

∵BE垂直平分AM

∴AB＝BM

在△ADM和△FCM中，∠AMD=∠FMC,∠DAF=∠F，AM=MF，

∴△ADM≌△FCM