Question

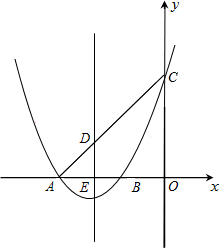如图，已知抛物线y=x²+4x+3交x轴于A、B两点，交y轴于点C，抛物线的对称轴交x轴于点E，点B的坐标为（-1，0）．
（1）求抛物线的对称轴及点A的坐标；
（2）在平面直角坐标系xoy中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；
（3）连接CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．

Answer 1

分析：（1）根据二次函数y=ax²+bx+c的对称轴为x=-

b

2a

，求得抛物线的对称轴，因为函数与X轴的交点是y=0，列方程即可求得；
（2）分别以AC，AB为对角线各可求得一点，再以AC，AB为边求得一点；
（3）首先可求得梯形DEOC的面积，根据题意：在OE上找点F，使OF=

4

3

，此时S_△COF=

1

2

×

4

3

×3=2，直线CF把四边形DEOC分成面积相等的两部分，交抛物线于点M，设直线CM的解析式为y=kx+3，它经过点F（-

4

3

，0），则-

4

3

k+3=0（11分）解之，得k=

9

4

∴直线CM的解析式为y=

9

4

x+3．

解答：解：（1）①对称轴x=-

4

2

=-2；
②当y=0时，有x²+4x+3=0，
解之，得x₁=-1，x₂=-3，
∴点A的坐标为（-3，0）．

（2）满足条件的点P有3个，分别为（-2，3），（2，3），（-4，-3）．

（3）存在．
当x=0时，y=x²+4x+3=3
∴点C的坐标为（0，3），
∵DE∥y轴，AO=3，EO=2，AE=1，CO=3，
∴△AED∽△AOC
∴

AE

AO

=

DE

CO

即

1

3

=

DE

3

，
∴DE=1．
∴S_梯形DEOC=

1

2

（1+3）×2=4，
在OE上找点F，使OF=

4

3

，
此时S_△COF=

1

2

×

4

3

×3=2，直线CF把四边形DEOC分成面积相等的两部分，交抛物线于点M．
设直线CM的解析式为y=kx+3，它经过点F（-

4

3

，0）．
则-

4

3

k+3=0，（11分）
解之，得k=

9

4

，
∴直线CM的解析式为y=

9

4

x+3．

点评：此题属于中考中的压轴题，难度较大，知识点考查的较多而且联系密切，需要学生认真审题．此题考查了二次函数与一次函数，四边形的综合知识，解题的关键是要注意数形结合思想的应用．