题目内容
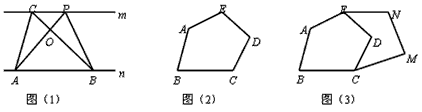
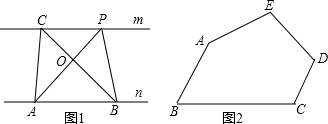
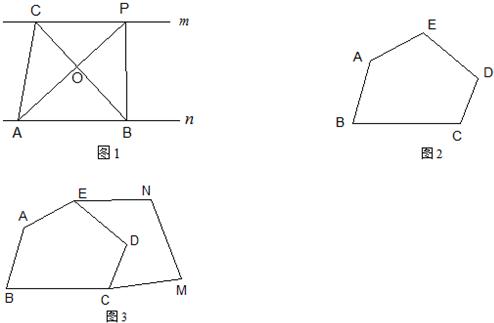
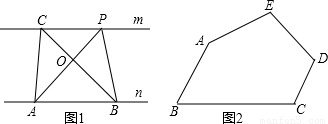
探究规律：如图1，已知直线m∥n，A、B为直线n上的两点，C、P为直线m上的两点．
（1）请写出图中面积相等的各对三角形：______；
（2）如果A、B、C为三个定点，点P在m上移动，那么无论P点移动到任何位置总有：______与△ABC的面积相等；理由是：______．
解决问题：
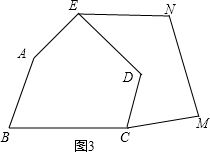
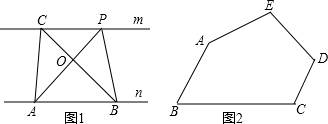
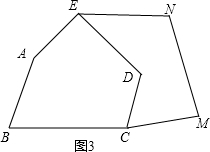
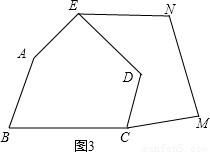
如图2，五边形ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图3所示的形状，但承包土地与开垦荒地的分界小路（图3中折线CDE）还保留着，张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案．（不计分界小路与直路的占地面积）
（1）写出设计方案，并在图3中画出相应的图形；
（2）说明方案设计理由．
（1）请写出图中面积相等的各对三角形：______；
（2）如果A、B、C为三个定点，点P在m上移动，那么无论P点移动到任何位置总有：______与△ABC的面积相等；理由是：______．
解决问题：
如图2，五边形ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图3所示的形状，但承包土地与开垦荒地的分界小路（图3中折线CDE）还保留着，张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案．（不计分界小路与直路的占地面积）
（1）写出设计方案，并在图3中画出相应的图形；
（2）说明方案设计理由．
探究规律：
（1）△ABC和△ABP；△PCA和△PCB；△ACO和△PBO；
（2）△ABP，同底等高的两个三角形的面积相等．
解决问题：
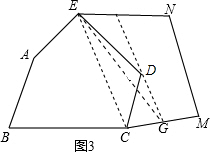
（1）连接EC，过D作EC的平行线DG交CM于点G，连接EG，EG就是所求的路，
（2）∵DG∥EC
∴S△EDC=S△ECG∴S△EDC+SABCE=S△ECG+SABCE
∴路两边的面积相等．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
PAB与△ABC的面积相等；理由是：__________．