题目内容
(1)如图,已知?ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.求证:CD=FA;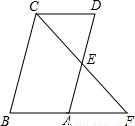
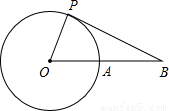
(2)如图,A是半径为12cm的⊙O上的定点,点B是OA延长线上的一点,动点P从A出发,以2πcm/s的速度沿圆周逆时针运动,且当点P运动的时间为2s时,直线BP恰与⊙O相切.求:∠B的度数.
【答案】分析:(1)要证明CD=FA,只要转化为证明△CDE≌△FAE即可;
(2)根据已知易得弧AP的长度,根据弧长公式即可求得∠O的度数,根据切线的性质,易得∠OPB=90°,则∠B即可求得.
解答:(1)证明:
∵?ABCD中,CD∥AB,
∴∠CDE=∠FAE,∠DCE=∠AFE.(1分)
又∵DE=AE,
∴△CDE≌△FAE(AAS).(2分)
∴CD=FA.(3分)
(2)解:弧长为2π×2=4π,周长为24π,(4分)
∠POA= ×360°=60°.(5分)
×360°=60°.(5分)
∵直线BP恰与⊙O相切,
∴∠OPB=90°.(6分)
∴∠PB0=30°.(7分)
点评:证明三角形全等是证明线段相等的常用方法,并且本题考查了弧长公式,是一个基础题目.
(2)根据已知易得弧AP的长度,根据弧长公式即可求得∠O的度数,根据切线的性质,易得∠OPB=90°,则∠B即可求得.
解答:(1)证明:
∵?ABCD中,CD∥AB,
∴∠CDE=∠FAE,∠DCE=∠AFE.(1分)
又∵DE=AE,
∴△CDE≌△FAE(AAS).(2分)
∴CD=FA.(3分)
(2)解:弧长为2π×2=4π,周长为24π,(4分)
∠POA=
 ×360°=60°.(5分)
×360°=60°.(5分)∵直线BP恰与⊙O相切,
∴∠OPB=90°.(6分)
∴∠PB0=30°.(7分)
点评:证明三角形全等是证明线段相等的常用方法,并且本题考查了弧长公式,是一个基础题目.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=