题目内容
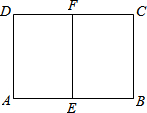矩形ABCD中，E、F分别是AB、CD的中点，且矩形ABCD与矩形EFCB相似，AB=a，则BC=
| ||
| 2 |
| ||
| 2 |
分析：利用相似多边形的对应边的比相等列出比例式求解即可．
解答：解：矩形ABCD对折后所得矩形与原矩形相似，
∵矩形ABCD∽矩形BCFE，
∵E、F分别为AB、CD的中点，
∴矩形ABCD的面积是矩形BCFE面积的2倍，
设，AB=a，
∵E、F分别为AB、CD的中点，
∴
=
即：
=
，
得：BC=
a．
∵矩形ABCD∽矩形BCFE，
∵E、F分别为AB、CD的中点，
∴矩形ABCD的面积是矩形BCFE面积的2倍，
设，AB=a，
∵E、F分别为AB、CD的中点，
∴
| AD |
| AB |
| BE |
| BC |
即：
| BC |
| a |
| ||
| BC |
得：BC=
| ||
| 2 |
点评：本题考查相似多边形相似的性质及判定两个图形相似的依据：对应边的比相等，对应角相等，两个条件必须同时具备．
练习册系列答案
阅读快车系列答案
相关题目
（2012•建邺区一模）如图，矩形ABCD中，A（-4，1），B（0，1），C（0，3），则D点坐标是
（2013•西城区一模）如图，在矩形ABCD中，AB=2，BC=4．将矩形ABCD绕点C沿顺时针方向旋转90°后，得到矩形FGCE（点A、B、D的对应点分别为点F、G、E）．动点P从点B开始沿BC-CE运动到点E后停止，动点Q从点E开始沿EF-FG运动到点G后停止，这两点的运动速度均为每秒1个单位．若点P和点Q同时开始运动，运动时间为x（秒），△APQ的面积为y，则能够正确反映y与x之间的函数关系的图象大致是（ ）
（2013•连云港模拟）如图，在矩形ABCD中，DE平分∠ADC交BC于点E，EF⊥AD交AD于点F，若EF=3，AE=5，则AD=
