题目内容
如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，OE⊥OD．
（1）求∠BOD的度数；
（2）请通过计算说明OE是否平分∠BOC。
（1）求∠BOD的度数；
（2）请通过计算说明OE是否平分∠BOC。
（1）155°（2）OE平分∠BOC
解：(1)∵OD平分∠AOC
∴∠AOD=∠DOC=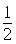
∠AOC=
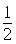
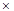50°="25°…………………" (2分)
∴∠BOD="180°-∠AOD=180°-25°=155°………………" (2分)
（2）∵∠DOE=90° ∠DOC=25°
∴∠COE=∠DOE-∠DOC=90°-25°=65°………………(2分)
又 ∵ ∠BOE=" ∠BOD" - ∠DOE=155°-90°=65°
∴ ∠COE=∠BOE
即OE平分∠BOC ………………………………………………(2分)
（1）由角平分线的性质即可推出∠AOD=25°，然后根据邻补角的性质即可推出∠BOD的度数，
（2）首先根据垂线的性质和（1）所得的结论，即可推出∠COE和∠BOE的度数，然后根据角平分线的定义即可确定OE平分∠BOC．
∴∠AOD=∠D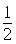OC=
∠AOC=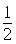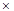50°="25°…………………" (2分)∴∠BOD="180°-∠AOD=180°-25°=155°………………" (2分)
（2）∵∠DOE=90° ∠DOC=25°
∴∠COE=∠DOE-∠DOC=90°-25°=65°………………(2分)
又 ∵ ∠BOE=" ∠BOD" - ∠DOE=155°-90°=65°
∴ ∠COE=∠BOE
即OE平分∠BOC ………………………………………………(2分)
（1）由角平分线的性质即可推出∠AOD=25°，然后根据邻补角的性质即可推出∠BOD的度数，
（2）首先根据垂线的性质和（1）所得的结论，即可推出∠COE和∠BOE的度数，然后根据角平分线的定义即可确定OE平分∠BOC．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
，（已知）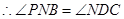
，（等量代换）
___________//__________，（ ）
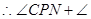_________=180°，（ ）
，（已知）
，（已知）
____________，（ ）
，（已知）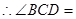
__________，（等量代换）
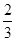还少40º，求这个角.
角后与它本身重合，那么
．36°； 
．45°； 
．72°； 
．90°．