题目内容
（2003•烟台）升国旗时，某同学站在离旗杆底部（DE）24米处行注目礼，当国旗升至旗杆顶端B时，该同学视线的仰角（∠BAC）恰为30°，若双眼离地面（AD）1.5米，则旗杆的高度为 米（结果保留3位小数）．
【答案】分析：旗杆的高度可分为该同学的身高和比身高高出的部分．比身高高的部分利用30°的正切值即可求得，加上身高即为旗杆的高度．
解答：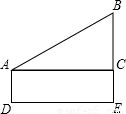
解：∵BC=AC×tan30°=DE×tan30°=
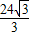=8
．
∴故旗杆的高度为BC+CE=BC+AD=8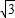
+1.5≈15.356（米）．
点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
解答：
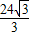解：∵BC=AC×tan30°=DE×tan30°==8．∴故旗杆的高度为BC+CE=BC+AD=8
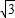+1.5≈15.356（米）．点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目