题目内容
如图,AB是⊙O的直径,CD是弦,且CD⊥AB于P,若CP=2,PB=1,则PA= 

4
连接OC,设OC=OB=r,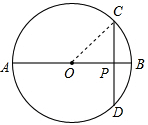
则OP=r-1,
在Rt△OCP中,由勾股定理得:OC2=OP2+CP2,
∴r2=(r-1)2+22,
r=5/2,
∴PA=2×5 /2-1=4,

则OP=r-1,
在Rt△OCP中,由勾股定理得:OC2=OP2+CP2,
∴r2=(r-1)2+22,
r=5/2,
∴PA=2×5 /2-1=4,

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目


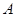 的坐标为
的坐标为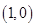 ,点
,点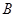 的坐标为
的坐标为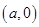 ,圆
,圆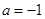 时,点
时,点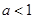 时,点
时,点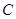 .当
.当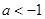 时,点
时,点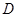 .当
.当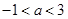 时,点
时,点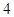 ,其中一个圆的半径长为
,其中一个圆的半径长为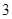 ,那么当两圆内切时,另一圆的半径为 .
,那么当两圆内切时,另一圆的半径为 .