题目内容
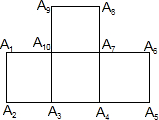
附加题:(1)如图,在四个正方形拼接成的图形中,以A1、A2、A3、…、A10这十个点中任意三点为顶点,共能组成______个等腰直角三角形.
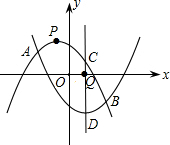
(2)已知y1=-ax2-ax+1的顶点P的纵坐标为 ,且与抛物线y2=ax2-ax-1相交于A,B两点.设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤x≤xB,过q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
,且与抛物线y2=ax2-ax-1相交于A,B两点.设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤x≤xB,过q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?

 解:(1)以A1为直角顶点的等腰直角三角形有2个,以A2为直角顶点的等腰直角三角形有1个,
解:(1)以A1为直角顶点的等腰直角三角形有2个,以A2为直角顶点的等腰直角三角形有1个,以A3为直角顶点的等腰直角三角形有4个,以A4为直角顶点的等腰直角三角形有4个,
以A5为直角顶点的等腰直角三角形有1个,以A6为直角顶点的等腰直角三角形有2个,
以A7为直角顶点的等腰直角三角形有6个,以A8为直角顶点的等腰直角三角形有3个,
以A9为直角顶点的等腰直角三角形有3个,以A10为直角顶点的等腰直角三角形有6个,故共有32个.
(2)解:a=
 .
.∵a=
 >0.
>0.∴抛物线y1开口向下,抛物线y2开口向上.
根据题意,得CD=y1-y2=(-
 x2-
x2- x+1)-(
x+1)-( x2-
x2- x-1)=-x2+2.
x-1)=-x2+2.∵xA≤x≤xB,
∴当x=0时,CD有最大值2.
分析:(1)设四个正方形的边长为1,经过试画探究,可以发现,所求的等腰直角三角形中,按边大小分,有三类:①以直角边长为1的18个;②直角边长为2的有2个;③直角边长为
 的有10个.
的有10个.(2)先根据抛物线y1的顶点纵坐标求出a的值,得a=
 ,因此y1开口向下,y2开口向上.那么CD的长可用y1-y2来表示,以此可得出一个关于CD长和x的函数关系式,根据函数的性质即可得出CD的最大值以及对应的x的值.
,因此y1开口向下,y2开口向上.那么CD的长可用y1-y2来表示,以此可得出一个关于CD长和x的函数关系式,根据函数的性质即可得出CD的最大值以及对应的x的值.点评:本题考查了规律性问题以及二次函数的综合应用.

练习册系列答案
相关题目
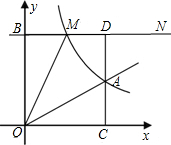 附加题:已知:如图,正比例函数y=ax的图象与反比例函数y=
附加题:已知:如图,正比例函数y=ax的图象与反比例函数y=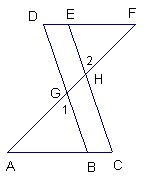 15、附加题:已知:如图∠1=∠2,∠C=∠D,试探究∠A=∠F相等吗?试说明理由.
15、附加题:已知:如图∠1=∠2,∠C=∠D,试探究∠A=∠F相等吗?试说明理由.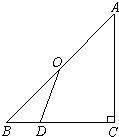 27、附加题:已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
27、附加题:已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.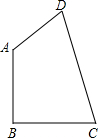 附加题:已知,如图,四边形ABCD中,AB=BC=1,CD=
附加题:已知,如图,四边形ABCD中,AB=BC=1,CD=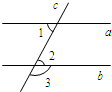 28、(附加题)已知:如图,a∥b,∠1=70°,则∠3的度数为
28、(附加题)已知:如图,a∥b,∠1=70°,则∠3的度数为