题目内容
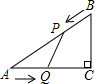 如图,在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题:
如图,在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题:(1)当t为何值时,以A、P、Q为顶点的三角形与△ABC相似?
(2)设四边形PQCB的面积为y(cm2),直接写出y与t之间的函数关系式;
(3)在点P、点Q的移动过程中,如果将△APQ沿其一边所在直线翻折,翻折后的三角形与△APQ组成一个四边形,那么是否存在某一时刻t,使组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
分析:(1)利用勾股定理求出AB,再根据题意知:AP=5-t,AQ=2t,当PQ∥BC,则△AQP∽△ACB,利用其对应边成比例即可求得t,当PQ⊥BC,则△APQ∽△ACB,利用其对应边成比例即可求得t.
(2)y=
t2-3t+6.
(3)若组成的四边形为菱形,则△APQ必为等腰三角形,有3种情况,①当沿AP翻折时,AQ=PQ,过Q作QD⊥AP于点D,则点D必为AP的中点,利用相似三角形对应边成比例即可求得;
②当沿PQ翻折时利用2t=5-t可解得t;
③当沿AQ翻折时,PQ=AP,过P点作PH⊥AC于H,则点H必为AQ的中点,利用相似三角形对应边成比例即可求得.
(2)y=
| 3 |
| 5 |
(3)若组成的四边形为菱形,则△APQ必为等腰三角形,有3种情况,①当沿AP翻折时,AQ=PQ,过Q作QD⊥AP于点D,则点D必为AP的中点,利用相似三角形对应边成比例即可求得;
②当沿PQ翻折时利用2t=5-t可解得t;
③当沿AQ翻折时,PQ=AP,过P点作PH⊥AC于H,则点H必为AQ的中点,利用相似三角形对应边成比例即可求得.
解答:解:(1)在Rt△ABC中,AB=
=5,
由题意知:AP=5-t,AQ=2t,
当PQ∥BC,则△AQP∽△ACB,
∴
=
,
∴
=
,
t=
,
<2,
当PQ⊥AB,则△APQ∽△ACB,
∴
=
,
∴
=
,
∴t=
,
<2,
∴当t=
或t=
时,
以A、P、Q为顶点的三角形与△ABC相似;
(2)过点P作PD⊥AC于D,
∵BC⊥AC,
∴PD∥BC,
∴
=
,
即
=
,
解得:PD=3-
t,
∴S四边形PQCB=S△ABC-S△APQ=
AC•BC-
AQ•PD=
×4×3-
×2t×(3-
t)=
t2-3t+6,
∴y=
t2-3t+6;
(3)若组成的四边形为菱形,则△APQ必为等腰三角形,
①当沿AP翻折时,AQ=PQ,过Q作QD⊥AP于点D,则点D必为AP的中点,
∴Rt△ADQ∽Rt△ACB,
∴
=
,
即
=
,解得t=
,
<2,
②当沿PQ翻折时,AQ=AP,2t=5-t,解得t=
<2
③当沿AQ翻折时,PQ=AP,过P点作PH⊥AC于H,则点H必为AQ的中点,
∴Rt△AHP∽Rt△ACB,
∴
=
即
=
,
解得:t=
>2(不合题意应舍去)
综上所述,当t=
或t=
时,所形成的四边形为菱形.
| BC2+AC2 |
由题意知:AP=5-t,AQ=2t,
当PQ∥BC,则△AQP∽△ACB,
∴
| AQ |
| AC |
| AP |
| AB |
∴
| 2t |
| 4 |
| 5-t |
| 5 |
t=
| 10 |
| 7 |
| 10 |
| 7 |
当PQ⊥AB,则△APQ∽△ACB,
∴
| AQ |
| AB |
| AP |
| AC |
∴
| 2t |
| 5 |
| 5-t |
| 4 |
∴t=
| 25 |
| 13 |
| 25 |
| 13 |
∴当t=
| 10 |
| 7 |
| 25 |
| 13 |
以A、P、Q为顶点的三角形与△ABC相似;

(2)过点P作PD⊥AC于D,
∵BC⊥AC,
∴PD∥BC,
∴
| PD |
| BC |
| PA |
| AB |
即
| PD |
| 3 |
| 5-t |
| 5 |
解得:PD=3-
| 3 |
| 5 |
∴S四边形PQCB=S△ABC-S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
∴y=
| 3 |
| 5 |
(3)若组成的四边形为菱形,则△APQ必为等腰三角形,
①当沿AP翻折时,AQ=PQ,过Q作QD⊥AP于点D,则点D必为AP的中点,
∴Rt△ADQ∽Rt△ACB,
∴
| AQ |
| AB |
| AD |
| AC |
即
| 2t |
| 5 |
| 5-t |
| 2×4 |
| 25 |
| 21 |
| 25 |
| 21 |
②当沿PQ翻折时,AQ=AP,2t=5-t,解得t=
| 5 |
| 3 |
③当沿AQ翻折时,PQ=AP,过P点作PH⊥AC于H,则点H必为AQ的中点,
∴Rt△AHP∽Rt△ACB,
∴
| AP |
| AB |
| AH |
| AC |
| 5-t |
| 5 |
| t |
| 4 |
解得:t=
| 20 |
| 9 |
综上所述,当t=
| 25 |
| 21 |
| 5 |
| 3 |
点评:此题涉及到的知识点较多,有勾股定理,相似三角形的判定与性质,菱形的判定,翻转变换等,综合性较强,又涉及上动点问题,给此题又增加了一定的难度,因此此题属于难题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图:在Rt△ACB中,∠C=90°,AC=8,BC=6,CD是斜边AB上的高.若点P在线段DB上,连接CP,sin∠APC=
如图:在Rt△ACB中,∠C=90°,AC=8,BC=6,CD是斜边AB上的高.若点P在线段DB上,连接CP,sin∠APC= 如图,在Rt△ACB中,∠C=90゜,点O为AB的中点,OE⊥OF交AC于E点、交BC于F点,EM⊥AB,FN⊥AB,垂足分别为M、N,
如图,在Rt△ACB中,∠C=90゜,点O为AB的中点,OE⊥OF交AC于E点、交BC于F点,EM⊥AB,FN⊥AB,垂足分别为M、N, 如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A=
如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A= 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于