题目内容
如图,是某城市部分街道示意图,ABCD是等腰梯形, 街道AD延伸后与街道EC相交于点F,且AF⊥EC,BA∥DE,BD∥AE,甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车, 路线是B→D→C→F;假设两车速度相同,途中耽误时间相同,那么谁先到达站,请说明理由。
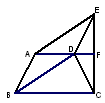
解 :甲乙同时到达F站;理由如下:
∵四边形ABCD是等腰梯形 ∴AB=DC
又∵AB∥DE,BD∥AE
∴四边形ABDE是平行四边形
∴AB=DE,AE=BD ∴DE=DC
又∵DF⊥EC ∴EF=CF
∵S甲=AB+AE+EF,S乙=BD+DC+CF ∴S甲=S乙
∴甲乙同时到达F站.
∵四边形ABCD是等腰梯形 ∴AB=DC
又∵AB∥DE,BD∥AE
∴四边形ABDE是平行四边形
∴AB=DE,AE=BD ∴DE=DC
又∵DF⊥EC ∴EF=CF
∵S甲=AB+AE+EF,S乙=BD+DC+CF ∴S甲=S乙
∴甲乙同时到达F站.

练习册系列答案
相关题目