题目内容
如图 ,梯形
,梯形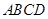 中,
中,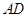 ∥
∥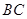 ,
,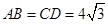 ,
,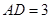 ,
,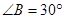 .动点
.动点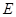 从点
从点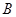 出发,以每秒
出发,以每秒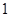 个单位长度的速度在线段
个单位长度的速度在线段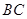 上运动;动点
上运动;动点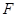 同时从点
同时从点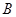 出发,以每秒
出发,以每秒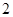 个单位长度的速度在线段
个单位长度的速度在线段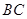 上运动.以
上运动.以 为边作等边△
为边作等边△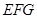 ,与梯形
,与梯形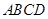 在线段
在线段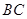 的同侧.设点
的同侧.设点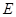 、
、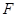 运动时间为
运动时间为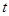 ,当点
,当点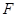 到达
到达 点时,运动结束.
点时,运动结束.
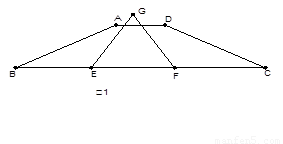
(1)当等边△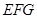 的边
的边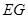 恰好经过点
恰好经过点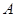 时,求运动时间
时,求运动时间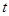 的值;
的值;
(2)在整个运动过程中,设等边△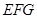 与梯形
与梯形 的重合部分面积为
的重合部分面积为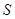 ,请直接写
,请直接写
出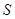 与
与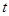 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量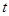 的取值范围;
的取值范围;
(3)如图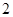 ,当点
,当点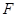 到达
到达 点时,将等边△
点时,将等边△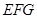 绕点
绕点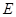 旋转
旋转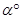 (
(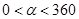 ),
),
直线 分别与直线
分别与直线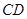 、直线
、直线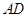 交于点
交于点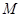 、
、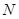 .是否存在这样的
.是否存在这样的 ,使△
,使△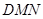 为等腰三角形?
为等腰三角形?
若存在,请求出此时线段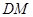 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
(1)t=4s(2)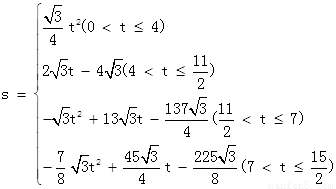 (3)存在。
(3)存在。
【解析】
试题分析:(1)当EG经过点A时 ∴△EGF为等边三角形∴∠AEF=600=∠B+∠BAE
∴∠BAE=∠B=300∴BE=AE=t=EF∴此时G与A,重合
∴在Rt△BAF中2t?cos300=4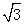 解得t=4s
解得t=4s
(2)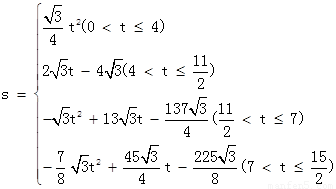 .
.
(3)存在;①当M点在线段CD上时,△DMN为等腰三角形
当MD=MN此时:∠C=∠1=∠N=∠CDN=300
∴ME=MC
作MH⊥CE

EH=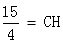
∴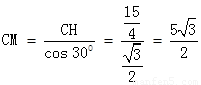
∴DM=
当D =D
=D 时
时
此时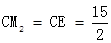
D =
= ,不存在
,不存在
当ND=NM时,则∠NDM=∠DMN=300,则M不在线段CD上. ∴舍
②当M在CD延长线上时当N1D=N1M1时∠1=∠M1,又∠1=∠2
∴∠2=∠ ∴EM1=CE=
∴EM1=CE=
过E作EH⊥CM1则CM1=2CH=2×CE?cos300=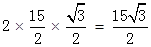

∴DM1=
当DM2=DN2时可知CM2=CE= ;∴DM2=
;∴DM2=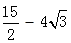
当M3D=M3N时此时∠M2N2D=∠1=30°
∴此时:∠M3EC=300
则M不在CD延长线上∴舍去
③当M在DC延长线上时
∵∠D为1500∴△DMN为等腰△时只有DM=DN
则:∠N=∠1=∠2=∠M
∴CE=CM= ∴DM=4
∴DM=4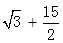
综上所述DM的长为: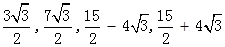
考点:动点问题
点评:本题难度较大,需要学生审题后通过动点在各范围内求出所对应函数式,再分情况具体分析,在分析过程中应抓住“动中有静”,即点移动过程中还会有一个量保持不变。此类题型多为中考的压轴题。

 名校课堂系列答案
名校课堂系列答案 如图,梯形中ABCD中,∠DBC=30°,
如图,梯形中ABCD中,∠DBC=30°,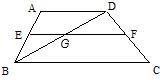 17、如图,梯形中位线的长是20cm,它被一条对角线分成的两部分的差是5cm,则这个梯形较长的底边长是( )
17、如图,梯形中位线的长是20cm,它被一条对角线分成的两部分的差是5cm,则这个梯形较长的底边长是( ) 如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为
如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为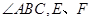 分别为AD、AB中点,点G为BC边上一点,且
分别为AD、AB中点,点G为BC边上一点,且
 中,
中,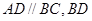 平分
平分 分别为AD、AB中点,点G为BC边上一点,且
分别为AD、AB中点,点G为BC边上一点,且
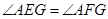 ;
; 时,四边形
时,四边形 为平行
为平行 四边形,并说明理由.
四边形,并说明理由.