题目内容
(10分)如图以O为圆心的两个同心圆,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B,小圆的切线AC与大圆相交于点D,且OC平分∠ACB.
【小题1】⑴试判断BC所在的直线与小圆的位置关系,并说明理由;
【小题2】⑵试判断线段AC、AD、BC之间的数量关系,并说明理由;
【小题3】⑶若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积
【小题1】相切,过O作OE⊥BC交BC交E得用角平分线性质证OE=OA
【小题2】⑵BC=AC+AD,连OD证△AOD≌△EOB
【小题3】⑶可得AC=6,由⑵得BE=4,S环形面积=π(OB2-OE2)=16π
解析考点:切线的判定与性质;全等三角形的判定与性质;勾股定理。
分析:
(1)只要证明OE垂直BC即可得出BC是小圆的切线,即与小圆的关系是相切。
(2)利用全等三角形的判定得出Rt△OAD≌Rt△OEB,从而得出EB=AD,从而得到三者的关系是前两者的和等于第三者。
(3)根据大圆的面积减去小圆的面积即可得到圆环的面积。
解答: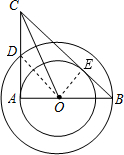
(1)BC所在直线与小圆相切。理由如下:
过圆心O作OE⊥BC,垂足为E;
∵AC是小圆的切线,AB经过圆心O,
∴OA⊥AC;
又∵CO平分∠ACB,OE⊥BC,
∴OE=OA,
∴BC所在直线是小圆的切线。
(2)AC+AD=BC。理由如下:
连接OD,
∵AC切小圆O于点A,BC切小圆O于点E,
∴CE=CA;
∵在Rt△OAD与Rt△OEB中,OA=OE,OD=OB,
∴Rt△OAD≌Rt△OEB,
∴EB=AD;
∵BC=CE+EB,
∴BC=AC+AD。
(3)∵∠BAC=90°,AB=8cm,BC=10cm,
∴AC=6cm;
∵BC=AC+AD,
∴AD=BC-AC=4cm,
∵圆环的面积为:S=π(OD)2-π(OA)2=π(OD2-OA2),
又∵OD2-OA2=AD2,
∴S=42π=16π(cm2)。




