题目内容
 1、如图,从甲地到乙地共有4条路可走,从乙地到丙地有3条路可走,从甲地到丙地有5条路可走,那么从甲地到丙地共有
1、如图,从甲地到乙地共有4条路可走,从乙地到丙地有3条路可走,从甲地到丙地有5条路可走,那么从甲地到丙地共有
17
条路可走.分析:从甲地到丙地可分两类办法;直达和转乙地.注:计数方法原理属于组合数学这门范畴,随着计算机科学的迅猛发展,教学学科原有的平衡被打破了,组合数学这门古老的数学学科又焕发出新的活力.
解答:解:甲地直达到丙地有5条路可走,
甲地转乙地到丙地有4×3=12条路可走,
则从甲地到丙地共有5+12=17条路可走.
故答案为:17.
甲地转乙地到丙地有4×3=12条路可走,
则从甲地到丙地共有5+12=17条路可走.
故答案为:17.
点评:本题考查了加法原理与乘法原理,使用乘法原理与加法原理的不同之处在于:在用加法原理时,完成一件事有几类方法,不论用哪一类方法,都能完成这件事;而用乘法原理时,完成一件事情可分为几步,只有每步都完成了,这件事情才得以完成.

练习册系列答案
相关题目
(本题满分9分)
下表是甲地到乙地两条线路的有关数据:
| 线路 | 绕路 | 直路 |
| 路程 | 300公里 | 180公里 |
| 过路费 | 30元 | 90元 |
(1)若小车的平均速度为80公里/小时,则小车走直路比走弯路节省多少时间?
(2)若小车每公里的油耗为![]() 升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
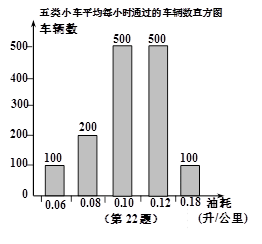
(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.
(本题满分9分)
下表是甲地到乙地两条线路的有关数据:
(1)若小车的平均速度为80公里/小时,则小车走直路比走弯路节省多少时间?
(2)若小车每公里的油耗为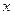 升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.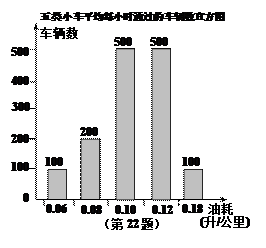
下表是甲地到乙地两条线路的有关数据:
| 线路 | 绕路 | 直路 |
| 路程 | 300公里 | 180公里 |
| 过路费 | 30元 | 90元 |
(2)若小车每公里的油耗为
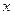 升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.

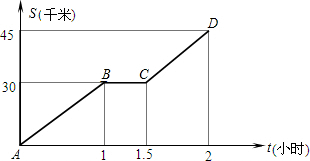 某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙埋正好用了2小时,已知摩托车行驶的路程S(千米)与行驶的时间t(小时)之间的函数关系由如图的图象ABCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油量
某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙埋正好用了2小时,已知摩托车行驶的路程S(千米)与行驶的时间t(小时)之间的函数关系由如图的图象ABCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油量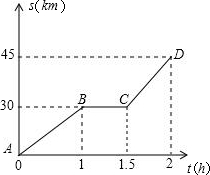 某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2h.已知摩托车行驶的路程s(km)与行驶的时间t(h)之间的函数关系如所示.若这辆摩托车平均每行驶100km的耗油量为2L,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油( )
某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2h.已知摩托车行驶的路程s(km)与行驶的时间t(h)之间的函数关系如所示.若这辆摩托车平均每行驶100km的耗油量为2L,根据图中给出的信息,从甲地到乙地,这辆摩托车共耗油( )