题目内容
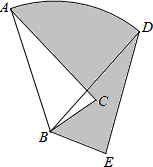（2013•贺州）如图，在△ABC中，AB=6，将△ABC绕点B顺时针旋转60°后得到△DBE，点A经过的路径为弧AD，则图中阴影部分的面积是6π
6π
．分析：图中阴影部分的面积=扇形ABD的面积+三角形DBE的面积-三角形ABC的面积．又由旋转的性质知△ABC≌△DBE，所以三角形DBE的面积=三角形ABC的面积．
解答：解：∵根据旋转的性质知∠ABD=60°，△ABC≌△DBE，
∴S△ABC-S△DBE，
∴S阴影=S扇形ABD+S△DBE-S△ABC=S扇形ABD=
=6π．
故答案是：6π．
∴S△ABC-S△DBE，
∴S阴影=S扇形ABD+S△DBE-S△ABC=S扇形ABD=
| 60π×62 |
| 360 |
故答案是：6π．
点评：本题考查了扇形面积的计算．解题的难点是找出图中阴影部分的面积=扇形ABD的面积+三角形DBE的面积-三角形ABC的面积．
练习册系列答案
相关题目
（2013•贺州）如图是一个几何体的三视图，根据图中提供的数据（单位：cm）可求得这个几何体的体积为（ ）
（2013•贺州）如图，在△ABC中，∠ABC=45°，AC=8cm，F是高AD和BE的交点，则BF的长是（ ）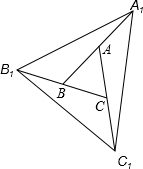
（2013•贺州）如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积
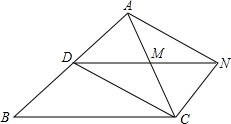（2013•贺州）如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC．