题目内容
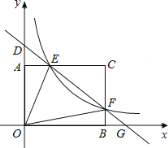
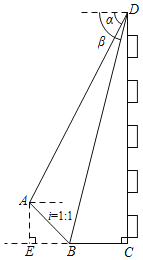
【题目】如图，某建筑物CD高96米，它的前面有一座小山，其斜坡AB的坡度为
．为了测量山顶A的高度，在建筑物顶端D处测得山顶A和坡底B的俯角分别为α、β．已知
，
，求山顶A的高度AE(C、B、E在同一水平面上)．
【答案】山顶A的高度AE为16米．
【解析】
作AF⊥CD于F．设AE=x米．由斜坡AB的坡度为i=1：1，得出BE=AE=x米．解Rt△BDC，求得
(米)，则AF=EC=（x+24）米．解Rt△ADF，得出DF=AFtanα=2（x+24）米，又DF=DC-CF=DC-AE=（96-x）米，列出方程2（x+24）=96-x，求出x即可．
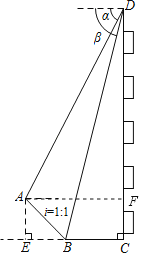
解：如图，作
于F．设
米．
∵斜坡AB的坡度为
，
∴
米．
在
中，∵
，
米，
，
∴(米)，
∴
米，
∴
米．
在
中，∵
，
，
∴
米，
∵
米，
∴
，解得
．
故山顶A的高度AE为16米．
练习册系列答案
名校课堂系列答案
相关题目
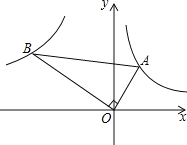
【题目】函数图象在探索函数的性质中有非常重要的作用，下面我们就一类特殊的函数展开探索．画函数
的图象，经历分析解析式、列表、描点、连线过程得到函数图象如图所示；经历同样的过程画函数
和
的图象如图所示．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣6 | ﹣4 | ﹣2 | 0 | ﹣2 | ﹣4 | ﹣6 | … |
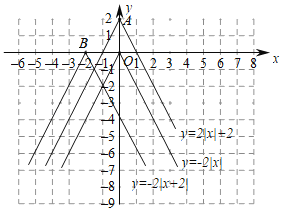
（1）观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解折式中绝对值前面的系数相同，则图象的开口方向和形状完全相同，只有最高点和对称轴发生了变化．写出点A，B的坐标和函数
的对称轴．
（2）探索思考：平移函数的图象可以得到函数和
的图象，分别写出平移的方向和距离．
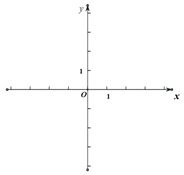
（3）拓展应用：在所给的平面直角坐标系内画出函数
和
在该函数图象上，且
，比较
，
的大小．
