题目内容
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心, PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax²+bx+4过A,B,C三点且AB=6.

⑴求⊙P的半径R的长;
⑵若点E在y轴上,且△ACE是等腰三角形,试写出所有点E的坐标;

⑴求⊙P的半径R的长;
⑵若点E在y轴上,且△ACE是等腰三角形,试写出所有点E的坐标;
(1)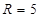 ;(2)
;(2)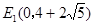 ,
,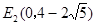 ,
,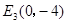 ,
,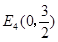
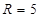 ;(2)
;(2)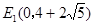 ,
,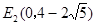 ,
,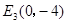 ,
,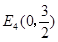
试题分析:(1)在函数y=ax2+bx+4中令x=0,解得y=4,则OC=PD=4,连接PA,在直角三角形△PAD中,根据勾股定理就可以得到PA的长.即圆的半径;
(2)根据等腰三角形的性质,把AC分别看作底和腰进行讨论.
(1)如图,连接AP
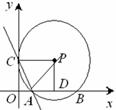
∵四边形ODPC为矩形
∴PD⊥AB
∴AD=BD=
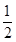 AB=3
AB=3又∵抛物线y=ax2+bx+4经过A,B,C三点
∴C(0,4)
即OC=4
∴PD=OC=4
∴由勾股定理得AP=5
∴⊙P的半径R的长为5;
(2)由(1)得OA=2,OC=4,则
 ,
,∵△ACE是等腰三角形,
∴
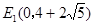 ,
,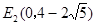 ,
,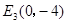 ,
,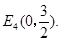
点评:解答本题的关键是熟练掌握垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.

练习册系列答案
相关题目
 ,点
,点 的坐标是
的坐标是 ,以点
,以点 为顶点的抛物线
为顶点的抛物线 经过
经过 轴上的点
轴上的点 .
.
 的坐标;
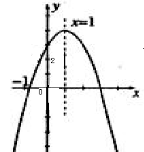
的坐标;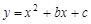 的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC长为__________ .
的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC长为__________ . 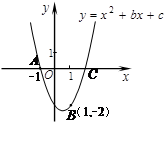
 的顶点坐标为 .
的顶点坐标为 . 的图象如图所示,则下列结论:
的图象如图所示,则下列结论:
 的两根之和大于1;②
的两根之和大于1;② ;
; 随
随 的增大而增大;④
的增大而增大;④ .
. 的图象与
的图象与 轴交点的坐标是
轴交点的坐标是  万元援助灾区
万元援助灾区 所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第
所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第 都是正整数)
都是正整数)
 时,该企业能援助多少所学校?
时,该企业能援助多少所学校? 万元的捐款,按照原来的分配方案援助其它学校.若
万元的捐款,按照原来的分配方案援助其它学校.若