题目内容
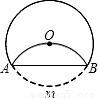
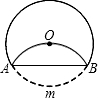 如图,将圆沿AB折叠后,圆弧恰好经过圆心,则
如图,将圆沿AB折叠后,圆弧恰好经过圆心,则 |
| AmB |
| A、60° | B、90° |
| C、120° | D、150° |
分析:利用折叠的特点,可得到点D为OE的中点,再利用直角三角形的性质,垂径定理及弧的度数等于它所对的圆心角的度数求解.
解答: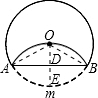 解:作OD⊥AB并延长OD交圆于点E,连接AO、OB,
解:作OD⊥AB并延长OD交圆于点E,连接AO、OB,
由题意知,OD=DE,OA=OB
∵OA=OE,
∴OD=
OA,
∴cos∠AOD=OD:OA=
,
∴∠AOD=60°,
∴∠AOB=120°,
即
的度数是120°.
故选C.
 解:作OD⊥AB并延长OD交圆于点E,连接AO、OB,
解:作OD⊥AB并延长OD交圆于点E,连接AO、OB,由题意知,OD=DE,OA=OB
∵OA=OE,
∴OD=
| 1 |
| 2 |
∴cos∠AOD=OD:OA=
| 1 |
| 2 |
∴∠AOD=60°,
∴∠AOB=120°,
即
 |
| AmB |
故选C.
点评:本题利用了折叠的特点、直角三角形的性质,垂径定理及弧的度数等于它所对的圆心角的度数等知识点.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
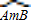 等于( )
等于( )
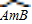 等于( )
等于( )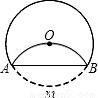
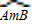 等于( )
等于( )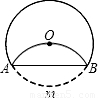
 等于( )
等于( )