题目内容
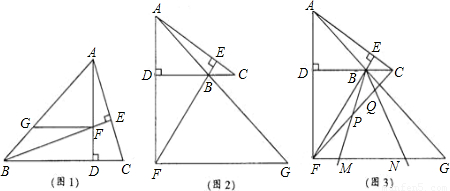
27、已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.
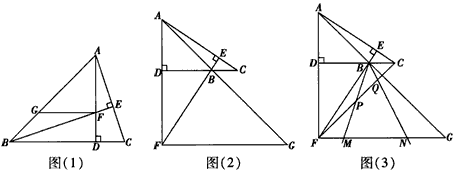
(1)如图1,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;
②FG+DC=AD;
(2)如图2,若∠ABC=135°,直接写出FG、DC、AD之间满足的数量关系.
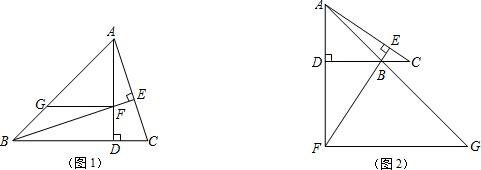
(1)如图1,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;
②FG+DC=AD;
(2)如图2,若∠ABC=135°,直接写出FG、DC、AD之间满足的数量关系.
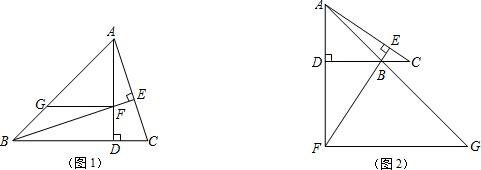
分析:(1)①要证明△BDF≌△ADC,如图,在△ABD中,∠ABC=45°,AD⊥BC,可证BD=AD,∠BDF=∠ADC;
在△ADC中,可证得∠AFE=∠ACD,又∵∠AFE=∠BFD(对顶角相等),∴∠ACD=∠BFD;运用AAS,问题可证.
②由△BDF≌△ADC可证得DF=DC;∵AD=AF+FD,∴AD=AF+DC;由GF∥BD,∠ABC=45°,可证得AF=GF;于是问题可证.
(2)∵∠ABC=135°,∴∠ABD=45°,△ABD、△AGF皆为等腰直角三角形,∴FG=AF=AD+DF;DF=DC可通过证明△BDF≌△ADC得到,故可得:FG=DC+AD.
在△ADC中,可证得∠AFE=∠ACD,又∵∠AFE=∠BFD(对顶角相等),∴∠ACD=∠BFD;运用AAS,问题可证.
②由△BDF≌△ADC可证得DF=DC;∵AD=AF+FD,∴AD=AF+DC;由GF∥BD,∠ABC=45°,可证得AF=GF;于是问题可证.
(2)∵∠ABC=135°,∴∠ABD=45°,△ABD、△AGF皆为等腰直角三角形,∴FG=AF=AD+DF;DF=DC可通过证明△BDF≌△ADC得到,故可得:FG=DC+AD.
解答:解:(1)①证明:∵∠ADB=90°,∠ABC=45°,
∴∠BAD=∠ABC=45°,∴AD=BD;
∵∠BEC=90°,∴∠CBE+∠C=90°
又∵∠DAC+∠C=90°,∴∠CBE=∠DAC;
∵∠FDB=∠CDA=90°,∴△FDB≌△CDA(ASA)
②∵△FDB≌△CDA,∴DF=DC;
∵GF∥BD,∴∠AGF=∠ABC=45°,
∴∠AGF=∠BAD,
∴FA=FG;
∴FG+DC=FA+DF=AD.
(2)FG、DC、AD之间的数量关系为:FG=DC+AD.
理由:∵∠ABC=135°,∴∠ABD=45°,△ABD、△AGF皆为等腰直角三角形,
∴BD=AD,FG=AF=AD+DF;
∵∠FAE+∠DFB=∠FAE+∠DCA=90°,
∴∠DFB=∠DCA;
又∵∠FDB=∠CDA=90°,BD=AD,
∴△BDF≌△ADC(AAS);
∴DF=DC,
∴FG、DC、AD之间的数量关系为:FG=DC+AD.
∴∠BAD=∠ABC=45°,∴AD=BD;
∵∠BEC=90°,∴∠CBE+∠C=90°
又∵∠DAC+∠C=90°,∴∠CBE=∠DAC;
∵∠FDB=∠CDA=90°,∴△FDB≌△CDA(ASA)
②∵△FDB≌△CDA,∴DF=DC;
∵GF∥BD,∴∠AGF=∠ABC=45°,
∴∠AGF=∠BAD,
∴FA=FG;
∴FG+DC=FA+DF=AD.
(2)FG、DC、AD之间的数量关系为:FG=DC+AD.
理由:∵∠ABC=135°,∴∠ABD=45°,△ABD、△AGF皆为等腰直角三角形,
∴BD=AD,FG=AF=AD+DF;
∵∠FAE+∠DFB=∠FAE+∠DCA=90°,
∴∠DFB=∠DCA;
又∵∠FDB=∠CDA=90°,BD=AD,
∴△BDF≌△ADC(AAS);
∴DF=DC,
∴FG、DC、AD之间的数量关系为:FG=DC+AD.
点评:本题综合考查了三角形全等的判定和性质;利用三角形全等证明线段相等是经常使用的重要方法,注意掌握.

练习册系列答案
相关题目

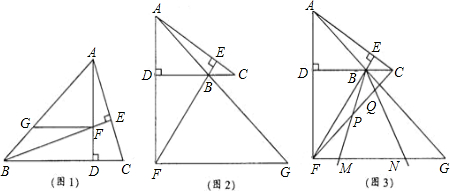
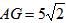 ,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图(3)),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若
,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图(3)),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若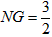 ,求线段PQ的长。
,求线段PQ的长。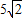 ,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图3),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若NG=
,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图3),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若NG= ,求线段PQ的长.
,求线段PQ的长.