题目内容
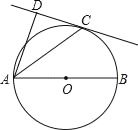
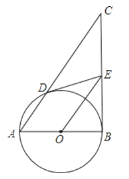
【题目】已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.
(1)如图,求证:EB=EC=ED;
(2)试问在线段DC上是否存在点F,满足BC2=4DFDC?若存在,作出点F,并予以证明;若不存在,请说明理由.
【答案】(1)见解析;(2)存在,理由见解析.
【解析】
(1)连接BD,已知ED、EB都是⊙O的切线,由切线长定理可证得OE垂直平分BD,而BD⊥AC(圆周角定理),则OE∥AC;由于O是AB的中点,可证得OE是△ABC的中位线,即E是BC中点,那么Rt△BDC中,DE就是斜边BC的中线,由此可证得所求的结论;(2)由(1)知:BC=2BE=2DE,则所求的比例关系式可转化为(![]() )2=DFDC,即DE2=DFDC,那么只需作出与△DEC相似的△DFE即可,这两个三角形的公共角为∠CDE,只需作出∠DEF=∠C即可;①∠DEC>∠C,即180°-2∠C>∠C,0°<∠C<60°时,∠DEF的EF边与线段CD相交,那么交点即为所求的F点;②∠DEC=∠C,即180°-2∠C=∠C,∠C=60°时,F与C点重合,F点仍在线段CD上,此种情况也成立;③∠DEC<∠C,即180°-2∠C<∠C,60°<∠C<90°时,∠DEF的EF边与线段的延长线相交,与线段CD没有交点,所以在这种情况下不存在符合条件的F点.
)2=DFDC,即DE2=DFDC,那么只需作出与△DEC相似的△DFE即可,这两个三角形的公共角为∠CDE,只需作出∠DEF=∠C即可;①∠DEC>∠C,即180°-2∠C>∠C,0°<∠C<60°时,∠DEF的EF边与线段CD相交,那么交点即为所求的F点;②∠DEC=∠C,即180°-2∠C=∠C,∠C=60°时,F与C点重合,F点仍在线段CD上,此种情况也成立;③∠DEC<∠C,即180°-2∠C<∠C,60°<∠C<90°时,∠DEF的EF边与线段的延长线相交,与线段CD没有交点,所以在这种情况下不存在符合条件的F点.
(1)证明:连接BD.
由于ED、EB是⊙O的切线,由切线长定理,得
ED=EB,∠DEO=∠BEO,
∴OE垂直平分BD.
又∵AB是⊙O的直径,
∴AD⊥BD.
∴AD∥OE.
即OE∥AC.
又O为AB的中点,
∴OE为△ABC的中位线,
∴BE=EC,
∴EB=EC=ED.
(2)解:在△DEC中,由于ED=EC,
∴∠C=∠CDE,
∴∠DEC=180°﹣2∠C.
①当∠DEC>∠C时,有180°﹣2∠C>∠C,即0°<∠C<60°时,在线段DC上存在点F
满足条件.
在∠DEC内,以ED为一边,作∠DEF,使∠DEF=∠C,且EF交DC于点F,则点F即为所求.
这是因为:
在△DCE和△DEF中,∵∠CDE=∠EDF,∠C=∠DEF,
∴△DEF∽△DCE.
∴DE2=DFDC.即(![]() BC)2=DFDC
BC)2=DFDC
∴BC2=4DFDC.
②当∠DEC=∠C时,△DEC为等边三角形,即∠DEC=∠C=60°,
此时,C点即为满足条件的F点,于是,DF=DC=DE,仍有BC2=4DE2=4DFDC.
③当∠DEC<∠C时,即180°﹣2∠C<∠C,60°<∠C<90°;所作的∠DEF>∠DEC,此时点F在DC的延长线上,故线段DC上不存在满足条件的点F.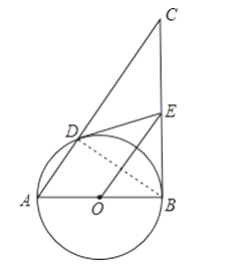

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案