题目内容
【题目】如图，在ABCD中，M、N是对角线BD上两点，且BN=DM．
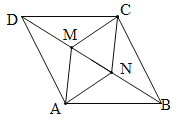
（1）求证：AM=CN；
（2）若AM⊥BD于M，AD=10，CN=6，求DM的长．
【答案】见解析；（2）DM=8.
【解析】
（1）根据平行四边形的性质及平行线的性质证明△ADM≌△CBN即可；
（2）根据全等三角形对应边相等得出AM的长．在Rt△AMD中，由勾股定理即可得出结论．
（1）∵ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠ADB=∠CBD．
在△ADM与△CBN中，∵AD=BC，∠ADB=∠CBD，DM=BN，∴△ADM≌△CBN，∴AM=CN；
（2）∵△ADM≌△CBN，∴AM=CN．
∵CN=6，∴AM=CN=6．
∵AM⊥BD，AD=10，AM=6，∴DM=
=8．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
【题目】某网络约车公司近期推出了“520专享”服务计划，即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”，为进一步提升服务品质，公司监管部门决定了解“单次营运里程”的分布情况．老王收集了本公司的5000个“单次营运里程”数据，这些里程数据均不超过25(千米)，他从中随机抽取了200个数据作为一个样本，整理、统计结果如下表，并绘制了不完整的频数分布直方图．
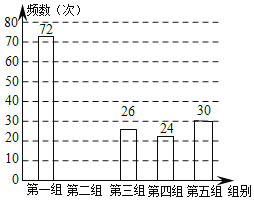
组别 | 单次营运里程“x”(千米) | 频数 |
第一组 | 0＜x≤5 | 72 |
第二组 | 5＜x≤10 | a |
第三组 | 10＜x≤15 | 26 |
第四组 | 15＜x≤20 | 24 |
第五组 | 20＜x≤25 | 30 |
根据以上信息，解答下列问题：
(1)表中a= ，样本中“单次营运里程”不超过15千米的频率为 ；
(2)请把频数分布直方图补充完整；
(3)估计该公司5000个“单次营运里程”超过20千米的次数．(写出解答过程)
