题目内容
在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),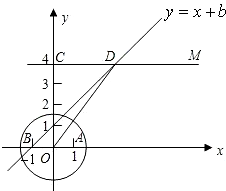 直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.
分析:(1)先求出点B的坐标,由直线过点B,把点B的坐标代入解析式,可求得b的值;点D在直线CM上,其纵坐标为4,利用求得的解析式确定该点的横坐标即可;
(2)△POD为等腰三角形,有三种情况:PO=OD,PO=PD,DO=DP,故需分情况讨论,要求点P的坐标,只要求出点P到原点O的距离即可;
(3)结合(2),可知⊙O的半径也需根据点P的不同位置进行分类讨论.
(2)△POD为等腰三角形,有三种情况:PO=OD,PO=PD,DO=DP,故需分情况讨论,要求点P的坐标,只要求出点P到原点O的距离即可;
(3)结合(2),可知⊙O的半径也需根据点P的不同位置进行分类讨论.
解答:解:(1)∵B与A(1,0)关于原点对称
∴B(-1,0)
∵y=x+b过点B
∴-1+b=0,b=1
∴y=x+1
当y=4时,x+1=4,x=3
∴D(3,4);
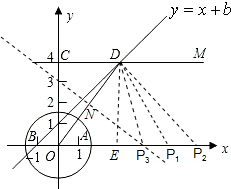
(2)作DE⊥x轴于点E,则OE=3,DE=4,
∴OD=
=
=5.
若△POD为等腰三角形,则有以下三种情况:
①以O为圆心,OD为半径作弧交x轴的正半轴于点P1,则OP1=OD=5,
∴P1(5,0).
②以D为圆心,DO为半径作弧交x轴的正半轴于点P2,则DP2=DO=5,
∵DE⊥OP2
∴P2E=OE=3,
∴OP2=6,
∴P2(6,0).
③取OD的中点N,过N作OD的垂线交x轴的正半轴于点P3,则OP3=DP3,
易知△ONP3∽△DCO.
∴
=
.
∴
=
,OP3=
.
∴P3(
,0).
综上所述,符合条件的点P有三个,分别是P1(5,0),P2(6,0),P3(
,0).
(3)①当P1(5,0)时,P1E=OP1-OE=5-3=2,OP1=5,
∴P1D=
=
=2
.
∴⊙P的半径为2
.
∵⊙O与⊙P外切,
∴⊙O的半径为5-2
.
②当P2(6,0)时,P2D=DO=5,OP2=6,
∴⊙P的半径为5.
∵⊙O与⊙P外切,
∴⊙O的半径为1.
③当P3(
,0)时,P3D=OP3=
,
∴⊙P的半径为
.
∵⊙O与⊙P外切,
∴⊙O的半径为0,即此圆不存在.
∴B(-1,0)
∵y=x+b过点B
∴-1+b=0,b=1
∴y=x+1
当y=4时,x+1=4,x=3
∴D(3,4);

(2)作DE⊥x轴于点E,则OE=3,DE=4,
∴OD=
| OE2+DE2 |
| 32+42 |
若△POD为等腰三角形,则有以下三种情况:
①以O为圆心,OD为半径作弧交x轴的正半轴于点P1,则OP1=OD=5,
∴P1(5,0).
②以D为圆心,DO为半径作弧交x轴的正半轴于点P2,则DP2=DO=5,
∵DE⊥OP2
∴P2E=OE=3,
∴OP2=6,
∴P2(6,0).
③取OD的中点N,过N作OD的垂线交x轴的正半轴于点P3,则OP3=DP3,
易知△ONP3∽△DCO.
∴
| OP3 |
| OD |
| ON |
| DC |
∴
| OP3 |
| 5 |
| ||
| 3 |
| 25 |
| 6 |
∴P3(
| 25 |
| 6 |
综上所述,符合条件的点P有三个,分别是P1(5,0),P2(6,0),P3(
| 25 |
| 6 |
(3)①当P1(5,0)时,P1E=OP1-OE=5-3=2,OP1=5,
∴P1D=
| P1E2+DE2 |
| 22+42 |
| 5 |
∴⊙P的半径为2
| 5 |
∵⊙O与⊙P外切,
∴⊙O的半径为5-2
| 5 |
②当P2(6,0)时,P2D=DO=5,OP2=6,
∴⊙P的半径为5.
∵⊙O与⊙P外切,
∴⊙O的半径为1.
③当P3(
| 25 |
| 6 |
| 25 |
| 6 |
∴⊙P的半径为
| 25 |
| 6 |
∵⊙O与⊙P外切,
∴⊙O的半径为0,即此圆不存在.
点评:本题考查了待定系数法求函数解析式,注意到分情况讨论是解决本题的关键.

练习册系列答案
相关题目
在直角坐标平面内的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向正前方沿直线行走a个单位长度.若机器人的位置在原点,正前方为y轴的负半轴,则它完成一次指令[2,60°]后位置的坐标为( )
A、(-1,
| ||
B、(-1,-
| ||
C、(-
| ||
D、(-
|
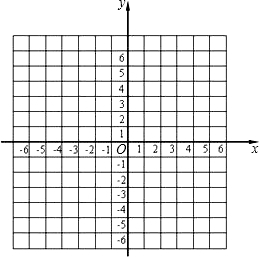 在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.