ЬтФПФкШн
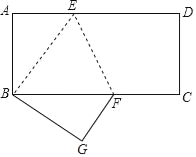
ЁОЬтФПЁПвбШчШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊ(6ЃЌ0)ЁЂЕуBЕФзјБъЮЊ(0ЃЌ8)ЃЌЕуCдкyжсЩЯЃЌзїжБЯпACЃЎЕуBЙигкжБЯпACЕФЖдГЦЕуBЁфИеКУдкxжсЩЯЃЌСЌНгCBЁфЃЎ
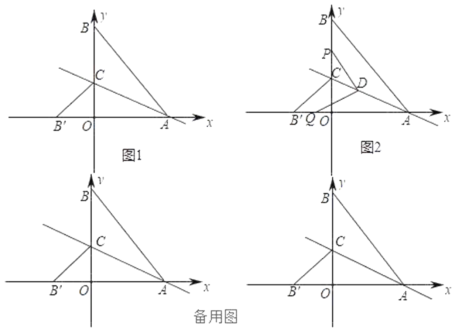
ЃЈ1ЃЉаДГіЕуBЁфЕФзјБъЃЌВЂЧѓГіжБЯпACЖдгІЕФКЏЪ§БэДяЪНЃЛ
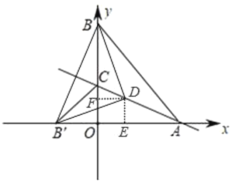
ЃЈ2ЃЉЕуDдкЯпЖЮACЩЯЃЌСЌНгDBЁЂDBЁфЁЂBBЁфЃЌЕБЁїDBBЁфЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓЕуDзјБъЃЛ
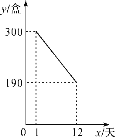
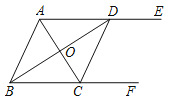
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуPДгЕуBГіЗЂвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђдЕуOдЫЖЏЃЌЕНДяЕуOЪБЭЃжЙдЫЖЏЃЌСЌНгPDЃЌЙ§DзїDPЕФДЙЯпЃЌНЛxжсгкЕуQЃЌЮЪЕуPдЫЖЏМИУыЪБЁїADQЪЧЕШбќШ§НЧаЮЃЎ
ЁОД№АИЁПЃЈ1ЃЉB'(Љ4ЃЌ0)ЃЌyЃНЉ![]() x+3ЃЛЃЈ2ЃЉD(2ЃЌ2)ЃЛЃЈ3ЃЉЕуPЕФдЫЖЏЪБМфЮЊ1УыЛђ5Љ
x+3ЃЛЃЈ2ЃЉD(2ЃЌ2)ЃЛЃЈ3ЃЉЕуPЕФдЫЖЏЪБМфЮЊ1УыЛђ5Љ![]() Уы
Уы
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЧѓГі![]() ЃЌИљОн
ЃЌИљОн![]() гы
гы![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЃЌЧѓГі
ЖдГЦЃЌЧѓГі![]() зјБъЃЌЩшЕу
зјБъЃЌЩшЕу![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌАбAЃЌCДњШыПЩЕУACБэДяЪНЃЛ
ЃЌАбAЃЌCДњШыПЩЕУACБэДяЪНЃЛ
ЃЈ2ЃЉгЩвбжЊПЩЕУ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌЙ§Еу
ЪЧЕШбќжБНЧШ§НЧаЮЃЌЙ§Еу![]() зї
зї![]() жсЃЌ
жсЃЌ![]() жсЃЌжЄУї
жсЃЌжЄУї ![]() ЃЌЕУГі
ЃЌЕУГі![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ДњШы
ДњШы![]() жаЃЌМДПЩЧѓГіЕуDзјБъЃЛ
жаЃЌМДПЩЧѓГіЕуDзјБъЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩЕУ![]() ЃЌжЄУї
ЃЌжЄУї![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌЗжЂйЕБ
ЃЌЗжЂйЕБ![]() ЪБЃЌЂкЕБ
ЪБЃЌЂкЕБ![]() ЪБЃЌЂлЕБ
ЪБЃЌЂлЕБ![]() ЪБЃЌШ§жжЧщПіЗжБ№НјааЬжТл.
ЪБЃЌШ§жжЧщПіЗжБ№НјааЬжТл.
НтЃКЃЈ1ЃЉЁпAЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЁЂЕуBЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌ
ЁрOAЃН6ЃЌOBЃН8ЃЌ
ЁпЁЯAOBЃН90ЁуЃЌ
ЁрABЃН10ЃЌ
ЁпBгыBЁфЙигкжБЯпACЖдГЦЃЌ
ЁрACДЙжБЦНЗжBBЁфЃЌ
ЁрBCЃНCBЁфЃЌAB'ЃНABЃН10ЃЌ
ЁрBЁфЃЈЉ4ЃЌ0ЃЉЃЌ
ЩшЕуCЃЈ0ЃЌmЃЉЃЌ
ЁрOCЃНmЃЌ
ЁрCBЁфЃНCBЃН8ЉmЃЌ
ЁпдкRtЁїCOBЁфжаЃЌЁЯCOBЁфЃН90ЁуЃЌ
Ёрm2+16ЃНЃЈ8ЉmЃЉ2ЃЌ
ЁрmЃН3ЃЌ
ЁрCЃЈ0ЃЌ3ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊyЃНkx+bЃЈkЁй0ЃЉЃЌ
АбAЃЈ6ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉДњШыПЩЕУkЃН-![]() ЃЌbЃН3ЃЌ
ЃЌbЃН3ЃЌ
ЁрyЃН-![]() x+3ЃЛ
x+3ЃЛ
ЃЈ2ЃЉЁпACДЙжБЦНЗжBBЁфЃЌ
ЁрDBЃНDBЁфЃЌ
ЁпЁїBDBЁфЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯBDBЁфЃН90ЁуЃЌ
Й§ЕуDзїDEЁЭxжсЃЌDFЁЭyжсЃЌ
ЁрЁЯDFOЃНЁЯDFBЃНЁЯDEBЁфЃН90ЁуЃЌ
ЁпЁЯEDFЃН360ЁуЉЁЯDFBЉЁЯDEOЉЁЯEOFЃЌЁЯEOFЃН90ЁуЃЌ
ЁрЁЯEDFЃН90ЁуЃЌ
ЁрЁЯEDFЃНЁЯBDBЁфЃЌ
ЁрЁЯBDFЃНЁЯEDBЁфЃЌ
ЁрЁїFDBЁеЁїEDBЁфЃЈAASЃЉЃЌ
ЁрDFЃНDEЃЌ
ЩшЕуDЃЈaЃЌaЃЉДњШыyЃНЉ![]() x+3жаЃЌ
x+3жаЃЌ
ЁрaЃН2ЃЌ
ЁрDЃЈ2ЃЌ2ЃЉЃЛ
ЃЈ3ЃЉЭЌЃЈ2ЃЉПЩЕУЁЯPDFЃНЁЯQDEЃЌ
ЁпDFЃНDEЃН2ЃЌЁЯPDFЃНЁЯQDEЃН90ЁуЃЌ
ЁрЁїPDFЁеЁїQDEЃЈAASЃЉЃЌ
ЁрPFЃНQEЃЌ
ЂйЕБDQЃНDAЪБЃЌ
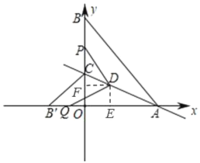
ЁпDEЁЭxжсЃЌ
ЁрQEЃНAEЃН4ЃЌ
ЁрPFЃНQEЃН4ЃЌ
ЁрBPЃНBFЉPFЃН2ЃЌ
ЁрЕуPдЫЖЏЪБМфЮЊ1УыЃЛ
ЂкЕБAQЃНADЪБЃЌ

ЁпAЃЈ6ЃЌ0ЃЉЁЂDЃЈ2ЃЌ2ЃЉЃЌ
ЁрADЃН2![]() ЃЌ
ЃЌ
ЁрAQЃН2![]() Љ4ЃЌ
Љ4ЃЌ
ЁрPFЃНQEЃН2![]() Љ4ЃЌ
Љ4ЃЌ
ЁрBPЃНBFЉPFЃН10Љ2![]() ЃЌ
ЃЌ
ЁрЕуPЕФдЫЖЏЪБМфЮЊ5Љ![]() УыЃЛ
УыЃЛ
ЂлЕБQDЃНQAЪБЃЌ
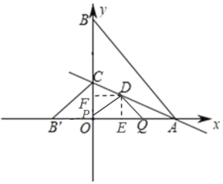
ЩшQEЃНnЃЌ
дђQDЃНQAЃН4ЉnЃЌ
дкRtЁїDEQжаЃЌЁЯDEQЃН90ЁуЃЌ
Ёр4+n2ЃНЃЈ4ЉnЃЉ2ЃЌ
ЁрnЃН1.5ЃЌ
ЁрPFЃНQEЃН1.5ЃЌ
ЁрBPЃНBF+PFЃН7.5ЃЌ
ЁрЕуPЕФдЫЖЏЪБМфЮЊ7.5УыЃЌ
Ёп0ЁмtЁм4ЃЌ
ЁрtЃН7.5ЩсШЅЃЌ
злЩЯЫљЪіЃКЕуPЕФдЫЖЏЪБМфЮЊ1УыЛђ5Љ![]() УыЃЎ
УыЃЎ

 КЎМйДѓДЎСЊЛЦЩНЪщЩчЯЕСаД№АИ
КЎМйДѓДЎСЊЛЦЩНЪщЩчЯЕСаД№АИ