题目内容
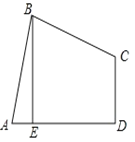
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( )
A.2B.3C.4D.5
【答案】C
【解析】
作BF⊥CD交CD的延长线于点F,根据直角三角形两锐角互余的关系可得∠ABE=∠CBF,利用AAS可证明△ABE≌△CBF,可得BE=BF;四边形ABCD的面积等于新正方形FBED的面积,根据∠BED=∠CDE=∠BFC=90°,可证明四边形BEDF是正方形,即可得BE=3.
过B作BF垂直DC的延长线于点F,
∵∠ABC=∠CDA=90°,BF⊥DF,
∴∠ABE+∠EBC=∠CBF+∠EBC,
∴∠ABE=∠CBF;
又∵BE⊥AD,BF⊥DF,且AB=BC,
∴△ABE≌△CBF,
∴BE=BF;四边形ABCD的面积等于四边形BEDF的面积
∵BE⊥AD,∠CDA=90°,DF⊥DF,
∴四边形BEDF是矩形,
又∵BE=BF,
∴四边形BEDF为正方形;
∵四边形ABCD的面积为16,
∴正方形BEDF的面积为16,
∴BE=4

故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在2020年元月的日历表中,某一天对应的号数的上、下、左、右四个数的和为![]() .
.
(1)如果某一天是![]() 号,请用含
号,请用含 ![]() 的代数式把
的代数式把![]() 表示出来;
表示出来;
(2)![]() 的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
(3)![]() 的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |