题目内容
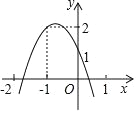
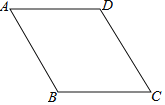
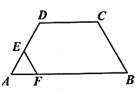
【题目】在四边形ABCD中,AB//DC,∠A=60°,AD=DC=BC=4,点E沿A→D→C→B运动,同时点F沿A→B→C运动,运动速度均为每秒1个单位,当两点相遇时,运动停止.则△AEF的面积y与运动时间x秒之间的图象大致为( )
A.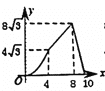 B.
B.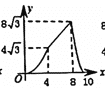 C.
C.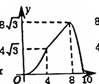 D.
D.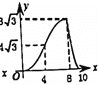
【答案】A
【解析】
分点E在AD上、点E在DC上, 点E在BC上运动时三种情况,分别求出函数表达式,进而求解.
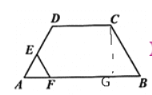
解:当0![]() x<4时,AE=AF=x,∠A=60°,∴三角形AEF是等边三角形.∴y=
x<4时,AE=AF=x,∠A=60°,∴三角形AEF是等边三角形.∴y=![]() x2.
x2.
当4![]() x<8时,点E在DC上,点F在AB上,AF=x,过点C作CG⊥AB,在Rt
x<8时,点E在DC上,点F在AB上,AF=x,过点C作CG⊥AB,在Rt![]() BCG中,∠B=60°,BC=4,则BG=2,CG=2
BCG中,∠B=60°,BC=4,则BG=2,CG=2![]() .∴y=
.∴y=![]() x
x![]() 2
2![]() =
=![]()
当8![]() x<10时,E,F均在BC上,则BE=12-x.BF=x-8,则E到AB的高为6
x<10时,E,F均在BC上,则BE=12-x.BF=x-8,则E到AB的高为6![]() -
-![]() x,点F到AB的高为
x,点F到AB的高为![]() x-4
x-4![]() .∴y=
.∴y=![]() 8[(6
8[(6![]() -
-![]() x)-(
x)-(![]() x-4
x-4![]() )]=-4
)]=-4![]() .故选A.
.故选A.

练习册系列答案
相关题目