题目内容
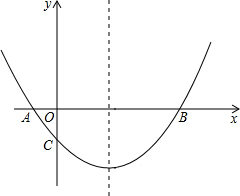 (2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,-
(2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,-| 5 | 2 |
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
分析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(-1,0),B(5,0),C(0,-
)三点代入求出a、b、c的值即可;
(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;
(3)分点N在x轴下方或上方两种情况进行讨论.
| 5 |
| 2 |
(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;
(3)分点N在x轴下方或上方两种情况进行讨论.
解答: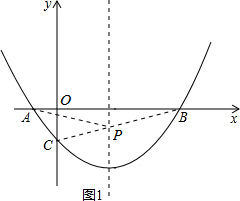 解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(-1,0),B(5,0),C(0,-
)三点在抛物线上,
∴
,
解得
.
∴抛物线的解析式为:y=
x2-2x-
;
(2)∵抛物线的解析式为:y=
x2-2x-
,
∴其对称轴为直线x=-
=-
=2,
连接BC,如图1所示,
∵B(5,0),C(0,-
),
∴设直线BC的解析式为y=kx+b(k≠0),
∴
,
解得
,
∴直线BC的解析式为y=
x-
,
当x=2时,y=1-
=-
,
∴P(2,-
);
(3)存在.
如图2所示,
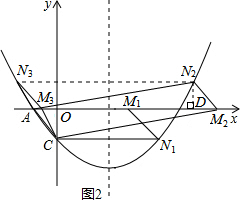
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,-
),
∴N1(4,-
);
②当点N在x轴上方时,
如图,过点N2作ND⊥x轴于点D,
在△AN2D与△M2CO中,
∴△AN2D≌△M2CO(ASA),
∴N2D=OC=
,即N2点的纵坐标为
.
∴
x2-2x-
=
,
解得x=2+
或x=2-
,
∴N2(2+
,
),N3(2-
,
).
综上所述,符合条件的点N的坐标为(4,-
),(2+
,
)或(2-
,
).
 解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(-1,0),B(5,0),C(0,-
| 5 |
| 2 |
∴
|
解得
|
∴抛物线的解析式为:y=
| 1 |
| 2 |
| 5 |
| 2 |
(2)∵抛物线的解析式为:y=
| 1 |
| 2 |
| 5 |
| 2 |
∴其对称轴为直线x=-
| b |
| 2a |
| -2 | ||
2×
|
连接BC,如图1所示,
∵B(5,0),C(0,-
| 5 |
| 2 |
∴设直线BC的解析式为y=kx+b(k≠0),
∴
|
解得
|
∴直线BC的解析式为y=
| 1 |
| 2 |
| 5 |
| 2 |
当x=2时,y=1-
| 5 |
| 2 |
| 3 |
| 2 |
∴P(2,-
| 3 |
| 2 |
(3)存在.
如图2所示,

①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,-
| 5 |
| 2 |
∴N1(4,-
| 5 |
| 2 |
②当点N在x轴上方时,
如图,过点N2作ND⊥x轴于点D,
在△AN2D与△M2CO中,
|
∴△AN2D≌△M2CO(ASA),
∴N2D=OC=
| 5 |
| 2 |
| 5 |
| 2 |
∴
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
解得x=2+
| 14 |
| 14 |
∴N2(2+
| 14 |
| 5 |
| 2 |
| 14 |
| 5 |
| 2 |
综上所述,符合条件的点N的坐标为(4,-
| 5 |
| 2 |
| 14 |
| 5 |
| 2 |
| 14 |
| 5 |
| 2 |
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,在解答(3)时要注意进行分类讨论.

练习册系列答案
相关题目
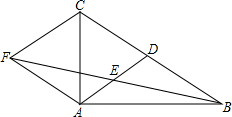 (2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.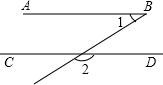 (2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
(2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
 (2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
(2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )