题目内容
如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为 .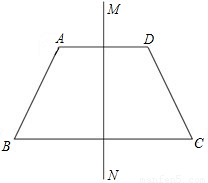
【答案】分析:根据已知得出四边形ABCD是等腰梯形,得出BC⊥MN,得出当P在NM和BC的交点上,Q在C上时,PQ+CQ最小,求出即可.
解答:解:∵AD∥BC,AB=CD,
∴梯形ABCD是等腰梯形,
∵MN是等腰梯形的对称轴,
∴BC⊥MN,
当P在NM和BC的交点上,Q在C上时,PQ+CQ最小,最小值是 ×6+0=3.
×6+0=3.
故答案为:3.
点评:本题考查了梯形和轴对称-最短路线问题的应用,关键是求出P和Q的位置,题目比较好,但是一道比较容易出错的题目.
解答:解:∵AD∥BC,AB=CD,
∴梯形ABCD是等腰梯形,
∵MN是等腰梯形的对称轴,
∴BC⊥MN,
当P在NM和BC的交点上,Q在C上时,PQ+CQ最小,最小值是
 ×6+0=3.
×6+0=3.故答案为:3.
点评:本题考查了梯形和轴对称-最短路线问题的应用,关键是求出P和Q的位置,题目比较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目
 如图,梯形中ABCD中,∠DBC=30°,
如图,梯形中ABCD中,∠DBC=30°, 如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为
如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为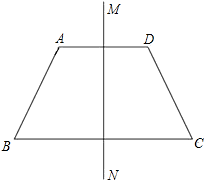 如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为________.
如图:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,Q为CD上一点,那么PQ+CQ的最小值为________.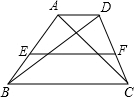 如图,梯形中ABCD中,∠DBC=30°,
如图,梯形中ABCD中,∠DBC=30°,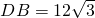 ,
,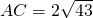 ,EF为梯形的中位线.求梯形的面积及EF的长.
,EF为梯形的中位线.求梯形的面积及EF的长.