题目内容
 (2013•德州一模)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(2013•德州一模)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长.
分析:(1)欲证明直线BF是⊙O的切线,只需证明∠ABF=90°;
(2)连接DO,EO.利用圆心角、弧、弦间的关系推知△AOD是等边三角形,根据等边三角形的性质知,在直角△ABF中,∠OAD=60°,AB=2AD=10,所以通过解该三角形即可求得线段BF的长度.
(2)连接DO,EO.利用圆心角、弧、弦间的关系推知△AOD是等边三角形,根据等边三角形的性质知,在直角△ABF中,∠OAD=60°,AB=2AD=10,所以通过解该三角形即可求得线段BF的长度.
解答: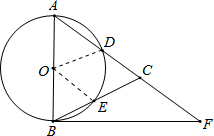 (1)证明:∵∠CBF=∠CFB,
(1)证明:∵∠CBF=∠CFB,
∴CB=CF.
又∵AC=CF,
∴CB=
AF,
∴△ABF是直角三角形.
∴∠ABF=90°,
∴直线BF是⊙O的切线;
(2)解:连接DO,EO.
∵点D,点E分别是弧AB的三等分点,
∴∠AOD=60°.
又∵OA=OD,
∴△AOD是等边三角形,∠OAD=60°,OA=AD=5.
又∵∠ABF=90°,AB=2OA=10,
∴BF=10
.
 (1)证明:∵∠CBF=∠CFB,
(1)证明:∵∠CBF=∠CFB,∴CB=CF.
又∵AC=CF,
∴CB=
| 1 |
| 2 |
∴△ABF是直角三角形.
∴∠ABF=90°,
∴直线BF是⊙O的切线;
(2)解:连接DO,EO.
∵点D,点E分别是弧AB的三等分点,
∴∠AOD=60°.
又∵OA=OD,
∴△AOD是等边三角形,∠OAD=60°,OA=AD=5.
又∵∠ABF=90°,AB=2OA=10,
∴BF=10
| 3 |
点评:本题考查了切线的判定、等边三角形的判定与性质等.解题时,充分利用了圆心角、弧、弦间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

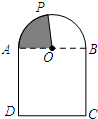 (2013•德州一模)如图是一个由正方形ABCD和半圆O组成的封闭图形,点O是圆心.点P从点A出发,沿弧AB,线段BC和线段CD,线段DA匀速运动,到达终点A.运动过程中OP扫过的面积(S)随时间(t)变化的图象大致是( )
(2013•德州一模)如图是一个由正方形ABCD和半圆O组成的封闭图形,点O是圆心.点P从点A出发,沿弧AB,线段BC和线段CD,线段DA匀速运动,到达终点A.运动过程中OP扫过的面积(S)随时间(t)变化的图象大致是( )